Dreisatz einfach erklärt: Beispiele und praktische Anwendungen
Stellen Sie sich vor, Sie möchten die Zutaten für ein Rezept verdoppeln, oder den Preis für eine bestimmte Menge berechnen. Wie machen Sie das am einfachsten? Die Antwort ist: mit dem Dreisatz! Der Dreisatz, auch bekannt als Regel de Tri, ist eine einfache, aber unglaublich nützliche Methode, um Proportionen zu berechnen und unbekannte Werte zu ermitteln.
Im Alltag begegnen uns ständig Situationen, in denen wir den Dreisatz anwenden können, ohne es vielleicht zu merken. Ob beim Einkaufen, beim Kochen oder beim Mischen von Farben – der Dreisatz hilft uns, schnell und einfach die richtigen Mengen zu bestimmen.
Dieser Artikel taucht tief in die Welt des Dreisatzes ein und erklärt Ihnen alles, was Sie darüber wissen müssen. Von den Grundlagen bis hin zu komplexeren Anwendungen, hier finden Sie eine umfassende Anleitung mit vielen Beispielen.
Der Dreisatz basiert auf der Idee der Proportionalität. Wenn zwei Größen proportional zueinander sind, bedeutet das, dass sie sich im gleichen Verhältnis verändern. Verdoppelt sich die eine Größe, verdoppelt sich auch die andere. Verdreifacht sich die eine Größe, verdreifacht sich auch die andere. Und so weiter.
Der Begriff "exemplos de regra de 3" ist die portugiesische Bezeichnung für "Beispiele der Regel von 3", was im Deutschen dem Dreisatz entspricht. Im Wesentlichen geht es darum, aus drei gegebenen Werten einen vierten, unbekannten Wert zu berechnen. Diese Methode ist so universell einsetzbar, dass sie in vielen Bereichen des täglichen Lebens, aber auch in der Wissenschaft und Technik Anwendung findet.
Die Geschichte des Dreisatzes reicht weit zurück. Bereits in alten babylonischen Texten finden sich Hinweise auf ähnliche Berechnungsmethoden. Im Laufe der Jahrhunderte wurde der Dreisatz immer weiter verfeinert und ist heute ein fester Bestandteil der Mathematik.
Ein einfaches Beispiel: Wenn 2 Äpfel 1 Euro kosten, wie viel kosten dann 4 Äpfel? Hier sind 2 Äpfel proportional zu 1 Euro und wir wollen den Preis für 4 Äpfel wissen. Mit dem Dreisatz können wir diesen Wert einfach berechnen.
Vorteile des Dreisatzes:
1. Einfachheit: Der Dreisatz ist leicht zu verstehen und anzuwenden, selbst ohne tiefere mathematische Kenntnisse.
2. Vielseitigkeit: Er kann in unzähligen Situationen eingesetzt werden, vom Kochen bis hin zu Finanzberechnungen.
3. Schnelligkeit: Der Dreisatz ermöglicht schnelle Berechnungen ohne komplizierte Formeln.
Schritt-für-Schritt-Anleitung:
1. Identifizieren Sie die drei gegebenen Werte und den gesuchten Wert.
2. Stellen Sie die Werte in einer Tabelle gegenüber.
3. Berechnen Sie den gesuchten Wert mithilfe der Kreuzmultiplikation.
Vor- und Nachteile des Dreisatzes
Häufig gestellte Fragen:
1. Was ist der Dreisatz? - Eine Methode zur Berechnung von Proportionen.
2. Wann kann ich den Dreisatz anwenden? - Immer wenn es um proportionale Beziehungen geht.
3. Ist der Dreisatz schwierig zu lernen? - Nein, er ist sehr einfach zu verstehen und anzuwenden.
4. Gibt es Alternativen zum Dreisatz? - Ja, aber der Dreisatz ist oft die einfachste Methode.
5. Wo finde ich weitere Informationen zum Dreisatz? - In Mathematikbüchern und online.
6. Wie kann ich den Dreisatz im Alltag nutzen? - Zum Beispiel beim Kochen, Einkaufen oder beim Umrechnen von Einheiten.
7. Was ist der Unterschied zwischen direktem und indirektem Dreisatz? - Beim direkten Dreisatz steigen beide Größen proportional, beim indirekten umgekehrt proportional.
8. Welche Fehler sollte ich beim Dreisatz vermeiden? - Falsche Zuordnung der Größen und Rechenfehler.
Tipps und Tricks: Achten Sie auf die Einheiten und stellen Sie sicher, dass die Größen proportional zueinander sind.
Zusammenfassend lässt sich sagen, dass der Dreisatz, oder "exemplos de regra de 3", ein äußerst nützliches Werkzeug für Berechnungen im Alltag und darüber hinaus ist. Seine Einfachheit und Vielseitigkeit machen ihn zu einer unverzichtbaren Methode für alle, die schnell und effektiv Proportionen berechnen möchten. Von einfachen Rezepten bis hin zu komplexeren Anwendungen – der Dreisatz bietet eine elegante Lösung für viele Probleme. Lernen Sie den Dreisatz und profitieren Sie von seinen Vorteilen! Üben Sie mit verschiedenen Beispielen und wenden Sie ihn in Ihrem Alltag an, um seine volle Kraft zu entdecken.
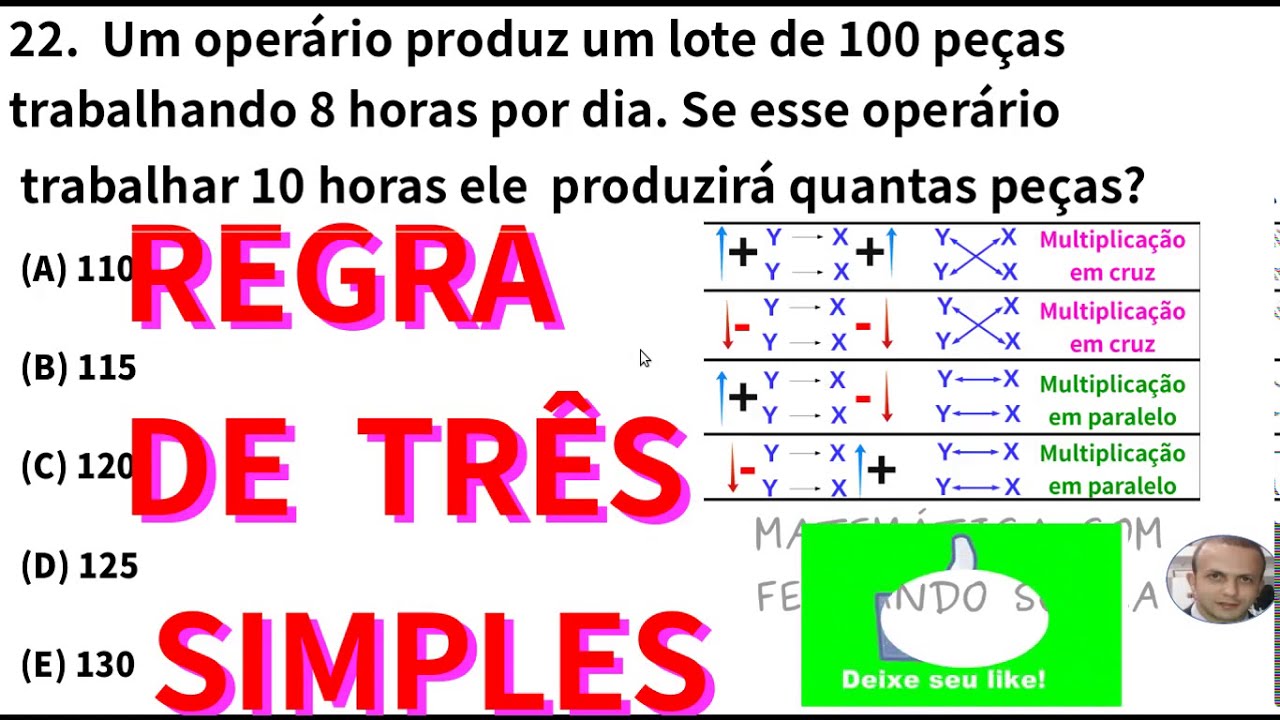
exemplos de regra de 3 | Kennecott Land

exemplos de regra de 3 | Kennecott Land

Por Que Como O Que | Kennecott Land

exemplos de regra de 3 | Kennecott Land

exemplos de regra de 3 | Kennecott Land

Razão e Proporção Archives | Kennecott Land

exemplos de regra de 3 | Kennecott Land

exemplos de regra de 3 | Kennecott Land

exemplos de regra de 3 | Kennecott Land

exemplos de regra de 3 | Kennecott Land

exemplos de regra de 3 | Kennecott Land

exemplos de regra de 3 | Kennecott Land

exemplos de regra de 3 | Kennecott Land

exemplos de regra de 3 | Kennecott Land

exemplos de regra de 3 | Kennecott Land