Konstante Funktionen: Ein unveränderlicher Wert in der Welt der Mathematik
Stellen Sie sich eine Welt vor, in der alles gleich bleibt. Keine Veränderung, keine Überraschungen. In der Mathematik gibt es ein solches Konzept: die konstante Funktion. Was aber verbirgt sich hinter diesem scheinbar einfachen Begriff?
Konstante Funktionen, auch als konstante Abbildungen bezeichnet, sind ein grundlegendes Element der Mathematik. Sie bilden die Basis für komplexere Konzepte und finden Anwendung in verschiedenen Bereichen, von der einfachen Algebra bis hin zur fortgeschrittenen Analysis. Ihre Einfachheit täuscht jedoch oft über ihre Bedeutung hinweg.
Dieser Artikel taucht tief in die Welt der konstanten Funktionen ein. Wir beleuchten ihre Definition, ihre Eigenschaften und ihre Bedeutung in verschiedenen mathematischen Kontexten. Von der Schulmathematik bis hin zu komplexeren Anwendungen, wir erforschen die verschiedenen Facetten dieser unveränderlichen mathematischen Größe.
Die Reise beginnt mit einer einfachen Frage: Was sind konstante Funktionen? Eine Funktion wird als konstant bezeichnet, wenn sie für jeden Eingabewert immer denselben Ausgabewert liefert. Egal, welche Zahl man in die Funktion eingibt, das Ergebnis bleibt stets gleich. Diese Unveränderlichkeit ist das charakteristische Merkmal konstanter Funktionen.
Die Geschichte der konstanten Funktionen ist eng mit der Entwicklung der Mathematik selbst verwoben. Seit den Anfängen der Algebra haben Mathematiker die Bedeutung von Konstanten und ihren Funktionen erkannt. Sie dienen als Grundlage für komplexere mathematische Strukturen und ermöglichen die Modellierung von unveränderlichen Größen in der realen Welt.
Eine konstante Funktion lässt sich mathematisch als f(x) = c definieren, wobei c eine Konstante ist. Zum Beispiel ist f(x) = 5 eine konstante Funktion, da sie für jeden Wert von x immer 5 zurückgibt. Grafisch dargestellt, ergibt eine konstante Funktion eine horizontale Linie, die den konstanten Wert auf der y-Achse repräsentiert.
Ein Vorteil konstanter Funktionen ist ihre Einfachheit. Sie sind leicht zu verstehen und zu berechnen. Ein weiterer Vorteil ist ihre Vorhersagbarkeit. Da der Ausgabewert immer gleich ist, lassen sich Ergebnisse leicht vorausbestimmen. Schließlich sind konstante Funktionen nützlich, um unveränderliche Größen in der realen Welt zu modellieren, wie z.B. den Festpreis eines Produkts.
Ein Beispiel: Ein Unternehmen verkauft jedes Produkt für 10€. Die Funktion, die den Preis eines Produkts beschreibt, ist f(x) = 10, wobei x die Anzahl der Produkte darstellt. Egal wie viele Produkte gekauft werden, der Preis pro Produkt bleibt konstant bei 10€.
Häufig gestellte Fragen:
1. Was ist eine konstante Funktion? Antwort: Eine Funktion, die für jeden Eingabewert denselben Ausgabewert liefert.
2. Wie wird eine konstante Funktion grafisch dargestellt? Antwort: Als horizontale Linie.
3. Was ist ein Beispiel für eine konstante Funktion? Antwort: f(x) = 7
4. Was sind die Vorteile von konstanten Funktionen? Antwort: Einfachheit, Vorhersagbarkeit, Modellierung unveränderlicher Größen.
5. Was ist die Ableitung einer konstanten Funktion? Antwort: 0
6. Wie unterscheidet sich eine konstante Funktion von einer linearen Funktion? Antwort: Eine lineare Funktion ändert ihren Wert mit der Eingabe, eine konstante Funktion nicht.
7. Können konstante Funktionen in der Physik angewendet werden? Antwort: Ja, zum Beispiel zur Darstellung von konstanten Kräften oder Geschwindigkeiten.
8. Wie kann man eine konstante Funktion erkennen? Antwort: An ihrem konstanten Ausgabewert, unabhängig von der Eingabe.
Tipps und Tricks: Denken Sie daran, dass die Ableitung einer konstanten Funktion immer Null ist. Dies ist ein wichtiges Konzept im Kalkül.
Konstante Funktionen mögen auf den ersten Blick trivial erscheinen, doch ihre Bedeutung in der Mathematik ist unbestreitbar. Sie bilden die Grundlage für komplexere Konzepte und bieten eine einfache Möglichkeit, unveränderliche Größen zu modellieren. Von der Schulmathematik bis hin zu komplexen wissenschaftlichen Anwendungen bieten konstante Funktionen ein wertvolles Werkzeug für das Verständnis und die Beschreibung der Welt um uns herum. Vertiefen Sie Ihr Verständnis der Mathematik, indem Sie die Einfachheit und Eleganz der konstanten Funktionen erforschen.

Wie kann ich aus einer Funktionsgleichung Werte bekommen rechnen | Kennecott Land

HILFE Was ist eine konstante Funktion Was bedeutet konstant | Kennecott Land

Ganzrationale Funktionen bestimmen Wie geht das Mathe Oberschule | Kennecott Land

Potenzfunktionen Polynomfunktionen zeichnen Eigenschaften erklären | Kennecott Land

Variation der Konstanten Erklärung und Beispiel mit Video | Kennecott Land

was sind konstante funktionen | Kennecott Land

was sind konstante funktionen | Kennecott Land

was sind konstante funktionen | Kennecott Land

Einstieg und erste Versuche mit Differentialrechnung | Kennecott Land
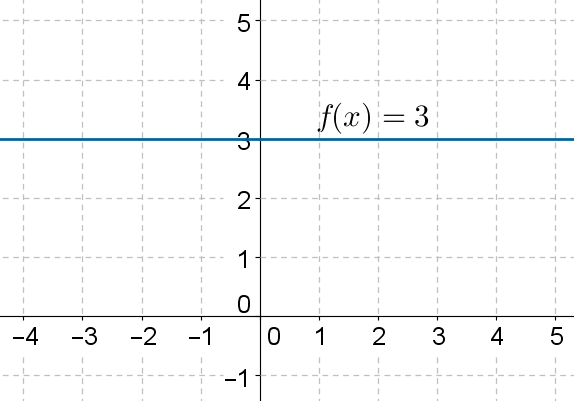
was sind konstante funktionen | Kennecott Land

Lineare Funktionen in Normalform | Kennecott Land

Bewegungen mit konstanter Beschleunigung | Kennecott Land

Lineare Funktionen fx mx b online lernen | Kennecott Land

was sind konstante funktionen | Kennecott Land

was sind konstante funktionen | Kennecott Land