Décryptage des relations entre X et Y sur une courbe
Qu'est-ce qui se cache derrière la danse subtile d'un point se déplaçant sur une courbe ? Comment décoder le langage secret des variables X et Y qui orchestrent ce ballet mathématique ? Ce voyage au cœur des graphiques nous dévoilera les mystères de la représentation visuelle des données et les relations fascinantes qu'elles révèlent.
La représentation de données à travers des courbes, où X et Y interagissent, est un pilier de la compréhension du monde qui nous entoure. De l'évolution des populations à la fluctuation des marchés financiers, en passant par la trajectoire d'une fusée, la relation entre X et Y sur une courbe nous permet de visualiser, d'analyser et de prédire des phénomènes complexes. Ce système de coordonnées, apparemment simple, est une fenêtre ouverte sur des univers de données.
L'histoire de la représentation graphique remonte à l'antiquité, avec des traces de cartographie et d'astronomie utilisant des systèmes de coordonnées rudimentaires. Cependant, c'est avec René Descartes et Pierre de Fermat au XVIIe siècle que le système de coordonnées cartésiennes, tel que nous le connaissons aujourd'hui, a véritablement pris forme. Cette innovation majeure a permis de traduire des équations algébriques en représentations visuelles, ouvrant la voie à une nouvelle ère de découvertes mathématiques et scientifiques.
L'importance de la visualisation des relations entre X et Y sur une courbe est indéniable. Un graphique permet de saisir d'un seul coup d'œil des tendances, des variations et des corrélations qui seraient difficiles à déceler dans un tableau de chiffres. Il facilite l'identification de points critiques, de maxima et de minima, et permet de modéliser des phénomènes pour en prédire l'évolution future.
Cependant, l'interprétation des courbes peut parfois être complexe. Des erreurs d'échelle, des données incomplètes ou une mauvaise compréhension des variables peuvent conduire à des conclusions erronées. Il est donc crucial de maîtriser les bases de l'analyse graphique et de faire preuve de discernement dans l'interprétation des données.
Prenons l'exemple simple d'une courbe représentant la distance parcourue par une voiture en fonction du temps. L'axe horizontal (X) représente le temps, tandis que l'axe vertical (Y) représente la distance. La pente de la courbe indique la vitesse de la voiture : plus la pente est raide, plus la voiture roule vite. Un plateau horizontal signifie que la voiture est à l'arrêt.
Les avantages de la représentation graphique sont nombreux : clarification des données, identification des tendances, facilitation de la comparaison et de la communication d'informations complexes. Imaginez essayer de comprendre l'évolution du cours d'une action sur plusieurs mois en consultant uniquement des tableaux de chiffres. Un simple graphique rend cette information instantanément accessible et compréhensible.
Pour analyser efficacement un graphique, il est essentiel de bien identifier les variables X et Y, de comprendre l'échelle utilisée et de rechercher les points clés, comme les intersections avec les axes, les maxima et les minima. L'utilisation d'outils d'analyse graphique peut également faciliter l'interprétation des données.
Avantages et Inconvénients de la représentation graphique
Un graphe permet de visualiser rapidement les variations de Y en fonction de X. Il permet de comprendre facilement l'évolution d'une valeur en fonction d'une autre, comme par exemple le prix d'un produit en fonction de la demande.
Voici quelques questions fréquemment posées :
1. Qu'est-ce qu'une courbe ? Une ligne continue représentant la relation entre deux variables.
2. Que représentent X et Y sur une courbe ? X représente généralement la variable indépendante et Y la variable dépendante.
3. Comment interpréter la pente d'une courbe ? La pente indique le taux de variation de Y par rapport à X.
4. Qu'est-ce qu'un point d'inflexion ? Un point où la courbe change de concavité.
5. Comment tracer une courbe à partir d'une équation ? En attribuant des valeurs à X et en calculant les valeurs correspondantes de Y.
6. Quels sont les différents types de courbes ? Linéaires, quadratiques, exponentielles, etc.
7. Comment utiliser un logiciel de graphique ? En entrant les données et en sélectionnant le type de graphique approprié.
8. Où trouver des ressources pour apprendre l'analyse graphique ? Des livres, des tutoriels en ligne et des logiciels spécialisés sont disponibles.
En conclusion, la représentation de la relation entre X et Y sur une courbe est un outil puissant pour comprendre et analyser les données. De la simple visualisation de tendances à la modélisation de phénomènes complexes, les graphiques nous permettent de décoder le langage des données et de prendre des décisions éclairées. Maîtriser l'art de l'interprétation graphique est essentiel dans un monde de plus en plus axé sur les données. N'hésitez pas à explorer les nombreuses ressources disponibles pour approfondir vos connaissances et exploiter pleinement le potentiel des courbes et des graphiques.

tracer un repère orthogonal o i j | Kennecott Land

Dm Jauge dun abreuvoir | Kennecott Land

Graphiques de fonctions séquence | Kennecott Land
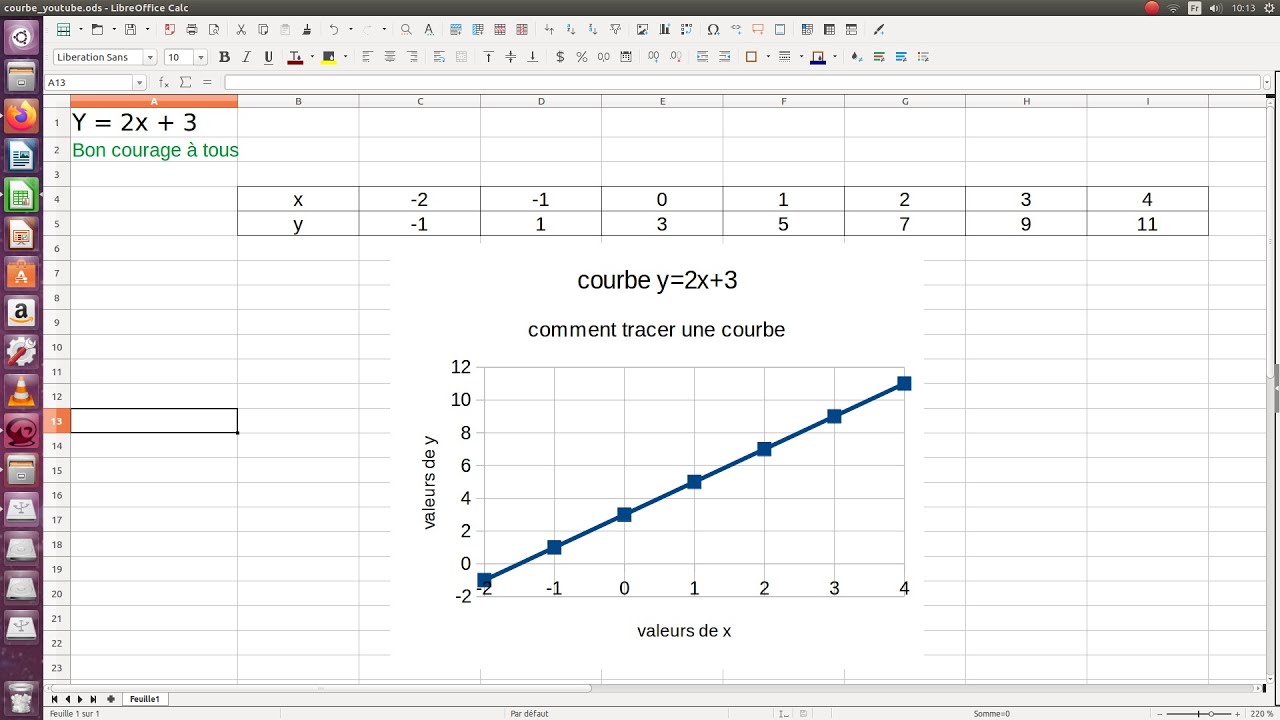
Comment Tracer Une Tangente Sur Excel | Kennecott Land

graphique en fonction de abscisse ordonnée | Kennecott Land

x et y sur une courbe | Kennecott Land

La Loi De Loffre Et De La Demande | Kennecott Land

Découvrir 163 imagen dérivabilité formule | Kennecott Land

Fonction De Graphique De Vecteur Photographie stock | Kennecott Land

Courbe de la fonction lnx | Kennecott Land

coefficient directeur dune droite formule | Kennecott Land

Sens de variation dune fonction numérique de la variable réelle | Kennecott Land

Courbe représentative dune fonction de la variable réelle dans un | Kennecott Land

tracer une droite déquation axbyc0 | Kennecott Land
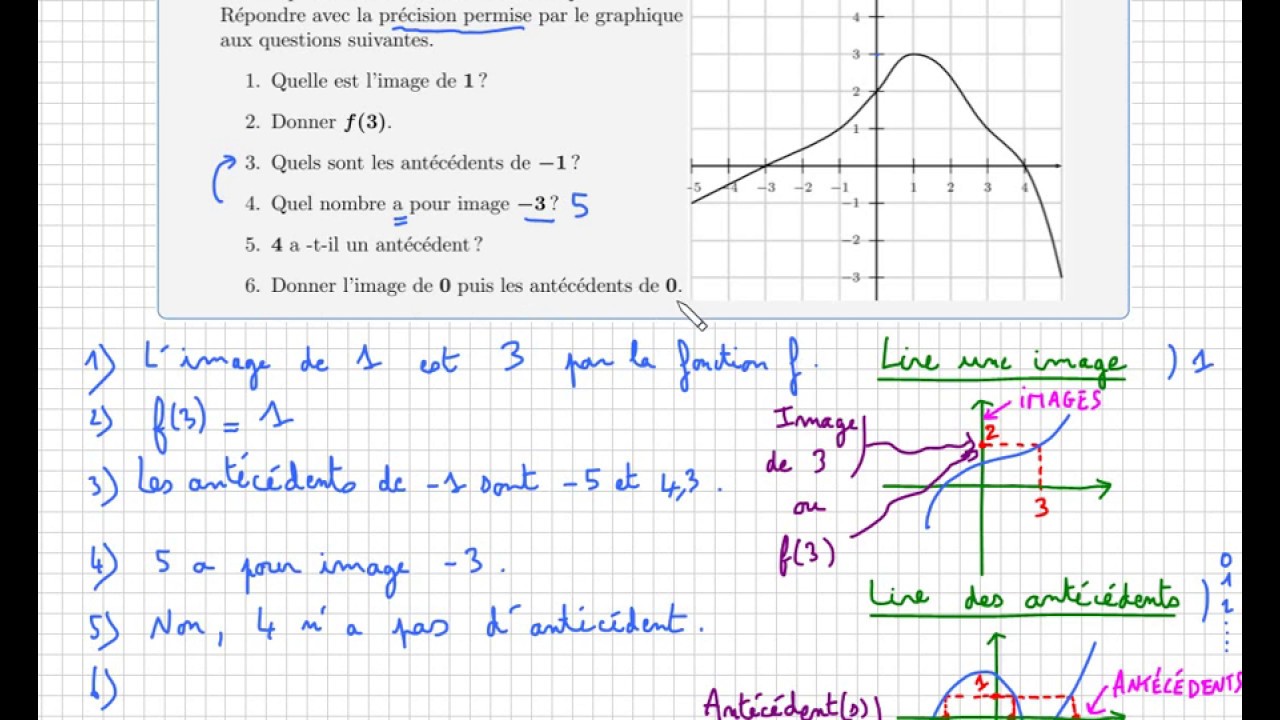
lire un antecedent sur une courbe | Kennecott Land