Calcolare l'area di un cilindro: guida completa e facile

15 Oct 2024

No autorizado conductor público como calcular el area de un circulo

Quante volte, osservando oggetti di uso comune come un bicchiere, una lattina o un tubo, ci siamo chiesti come calcolarne la superficie? La geometria, spesso considerata una materia astratta e distante dalla realtà, ci fornisce gli strumenti per rispondere a queste domande pratiche. In questo articolo, esploreremo il mondo dei cilindri e scopriremo come calcolarne l'area totale, un concetto che trova applicazione in molteplici campi, dalla progettazione industriale all'architettura.

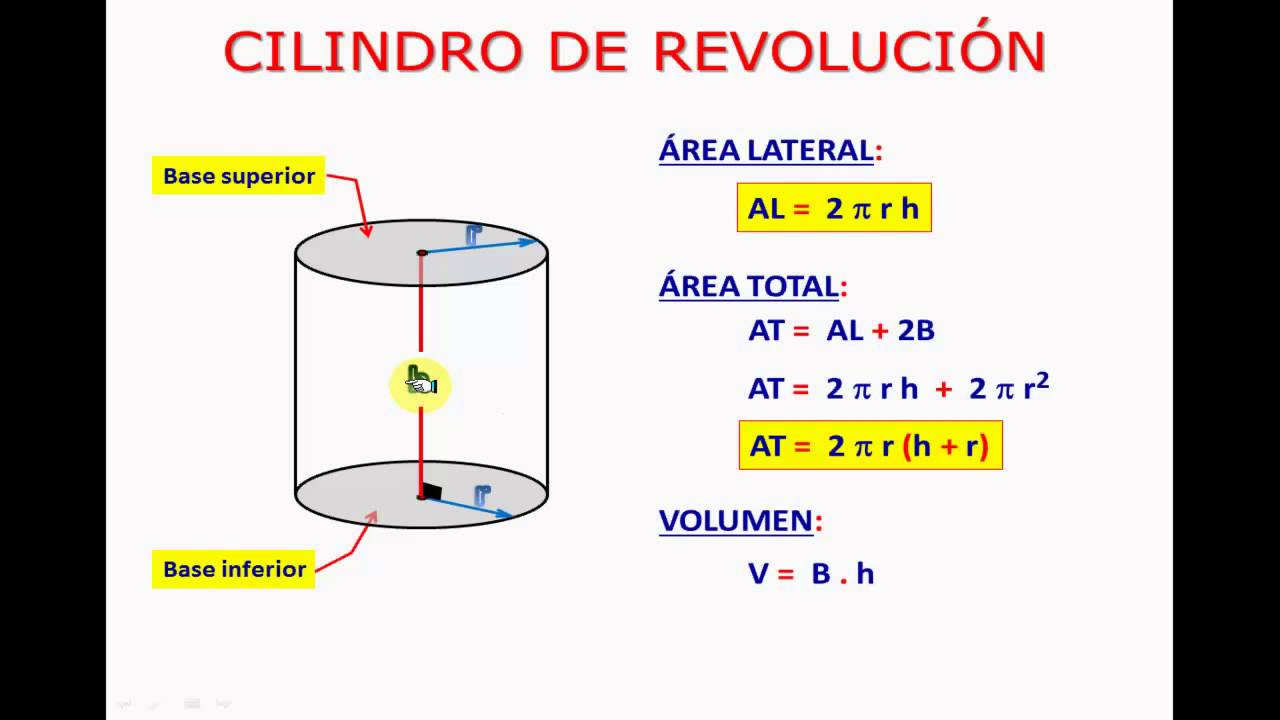
Il cilindro, solido geometrico caratterizzato da due basi circolari parallele e da una superficie laterale curva, è presente in innumerevoli oggetti della vita quotidiana. Per determinarne l'area totale, è necessario sommare l'area delle due basi all'area della superficie laterale. Ma come si calcolano queste aree?

Per calcolare l'area di ciascuna base, basta applicare la formula dell'area del cerchio: A = πr², dove r è il raggio del cerchio. La superficie laterale, invece, si ottiene "srotolando" il cilindro e ottenendo un rettangolo. La base di questo rettangolo corrisponde alla circonferenza della base del cilindro (2πr), mentre l'altezza del rettangolo coincide con l'altezza del cilindro (h). Quindi, l'area della superficie laterale è data da: 2πrh.

Riassumendo, l'area totale di un cilindro si calcola con la seguente formula:

Area totale = 2πr² + 2πrh

Dove:

• r = raggio della base del cilindro

• h = altezza del cilindro

Comprendere come calcolare l'area di un cilindro non è solo un esercizio intellettuale, ma ha importanti implicazioni pratiche. Ad esempio, nella progettazione di un silos per lo stoccaggio del grano, è fondamentale conoscere l'area della superficie laterale per determinare la quantità di materiale necessario per la sua costruzione. Allo stesso modo, un ingegnere che progetta un tubo per il trasporto di liquidi deve essere in grado di calcolare l'area della sezione trasversale per dimensionare correttamente il tubo in base al flusso desiderato.

Negli esempi concreti, spesso si utilizzano approssimazioni di π (pi greco) come 3.14 o 3.1416 per semplificare i calcoli. Esistono numerosi strumenti online, come calcolatori di area di cilindri, che permettono di ottenere risultati rapidi e precisi semplicemente inserendo i valori del raggio e dell'altezza.

Vantaggi e svantaggi di conoscere l'area di un cilindro

Sebbene non ci siano svantaggi diretti nel conoscere come calcolare l'area di un cilindro, potremmo dire che un eventuale svantaggio risiede nella complessità del calcolo nel caso di figure più complesse che includono cilindri come parte della loro struttura. In questi casi, la conoscenza della formula di base per l'area del cilindro diventa un prerequisito per affrontare calcoli più complessi.

Concludendo, la capacità di calcolare l'area di un cilindro è uno strumento prezioso in diversi ambiti, dimostrando come la geometria non sia solo una materia teorica, ma uno strumento pratico applicabile in molteplici situazioni reali. La prossima volta che incontrerete un oggetto cilindrico, potrete apprezzarne la forma geometrica e comprendere come calcolarne la superficie, connettendo la matematica al mondo che ci circonda.