Risolvere Sistemi di Equazioni: La Guida Completa al Metodo Grafico
Avete presente quel momento in cui vi trovate di fronte a due equazioni e vi sembra di dover scalare una montagna di numeri? Tranquilli, c'è un metodo che trasforma questa sfida in un gioco da ragazzi: la risoluzione grafica! Invece di perdersi in calcoli complicati, questo metodo ci permette di "vedere" la soluzione direttamente sul grafico.
Ma di cosa si tratta esattamente? In parole semplici, la risoluzione grafica di un sistema di equazioni consiste nel rappresentare graficamente le equazioni su uno stesso piano cartesiano. Il punto (o i punti) in cui le rette si intersecano rappresenta la soluzione del sistema, ovvero i valori che soddisfano entrambe le equazioni contemporaneamente.
Questo metodo è utile in diversi contesti, dalla matematica all'economia, dalla fisica all'ingegneria. Pensate ad esempio a dover calcolare il punto di equilibrio tra domanda e offerta di un prodotto: rappresentando graficamente le due curve, il punto di intersezione ci dirà esattamente il prezzo e la quantità di equilibrio.
Ma come si fa a mettere in pratica questo metodo? Per prima cosa, è importante saper tracciare il grafico di un'equazione lineare. Una volta disegnate entrambe le rette, basterà osservare il punto in cui si incontrano per trovare la soluzione. Se le rette sono parallele, significa che il sistema non ha soluzione; se invece coincidono, allora le soluzioni sono infinite.
La risoluzione grafica è un metodo intuitivo e visuale, che permette di avere una comprensione immediata della soluzione di un sistema di equazioni. Tuttavia, è importante ricordare che la precisione del risultato dipende dalla precisione del grafico. Per questo motivo, è sempre consigliabile verificare la soluzione trovata sostituendo i valori trovati nelle equazioni originali.
Vantaggi e Svantaggi della Risoluzione Grafica
| Vantaggi | Svantaggi |
|---|---|
| Intuitivo e visuale | Precisione limitata |
| Utile per una prima stima della soluzione | Difficoltà con sistemi di equazioni non lineari |
| Aiuta a comprendere il concetto di soluzione di un sistema | Richiede strumenti per il disegno grafico |
Ecco alcuni consigli utili per applicare al meglio la risoluzione grafica:
- Assicurarsi che le equazioni siano scritte in forma esplicita (y = mx + q).
- Scegliere una scala appropriata per gli assi del piano cartesiano.
- Tracciare i grafici con precisione, utilizzando una riga o un software apposito.
- Verificare sempre la soluzione trovata sostituendo i valori nelle equazioni originali.
- Esercitarsi con diversi esempi per acquisire sicurezza nel metodo.
Per concludere, la risoluzione grafica è un metodo efficace e intuitivo per risolvere sistemi di equazioni, soprattutto quando si ha a che fare con sistemi lineari. La sua natura visuale facilita la comprensione del concetto di soluzione e permette di ottenere una rapida stima dei risultati. Tuttavia, è importante ricordare che la precisione del metodo è limitata e che è sempre consigliabile verificare la soluzione trovata. Con un po' di pratica e di attenzione, la risoluzione grafica diventerà uno strumento prezioso nel vostro repertorio matematico.

Systems Of Equations Applications Worksheet | Kennecott Land

Graphing From Equations Worksheets | Kennecott Land

Solve Each System By Graphing Worksheets | Kennecott Land

Worksheet System Of Equation By Graphing | Kennecott Land

Systems Of Equations Graphing Worksheets | Kennecott Land
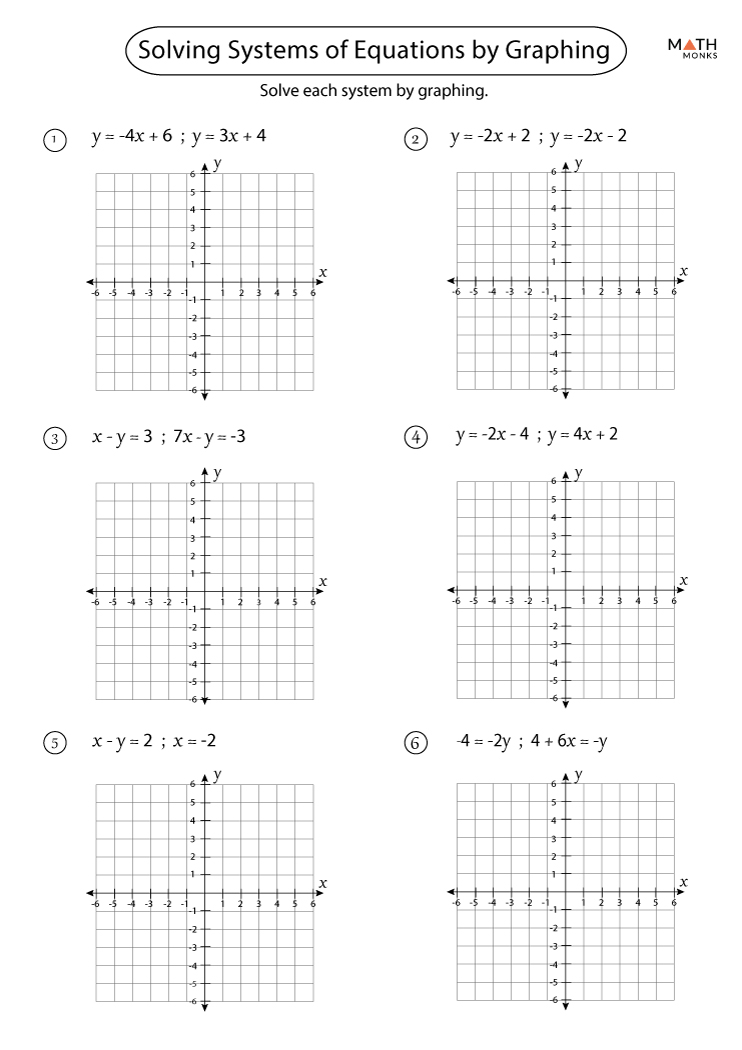
System Of Equations Worksheets | Kennecott Land

Solve Each System By Graphing Worksheet | Kennecott Land
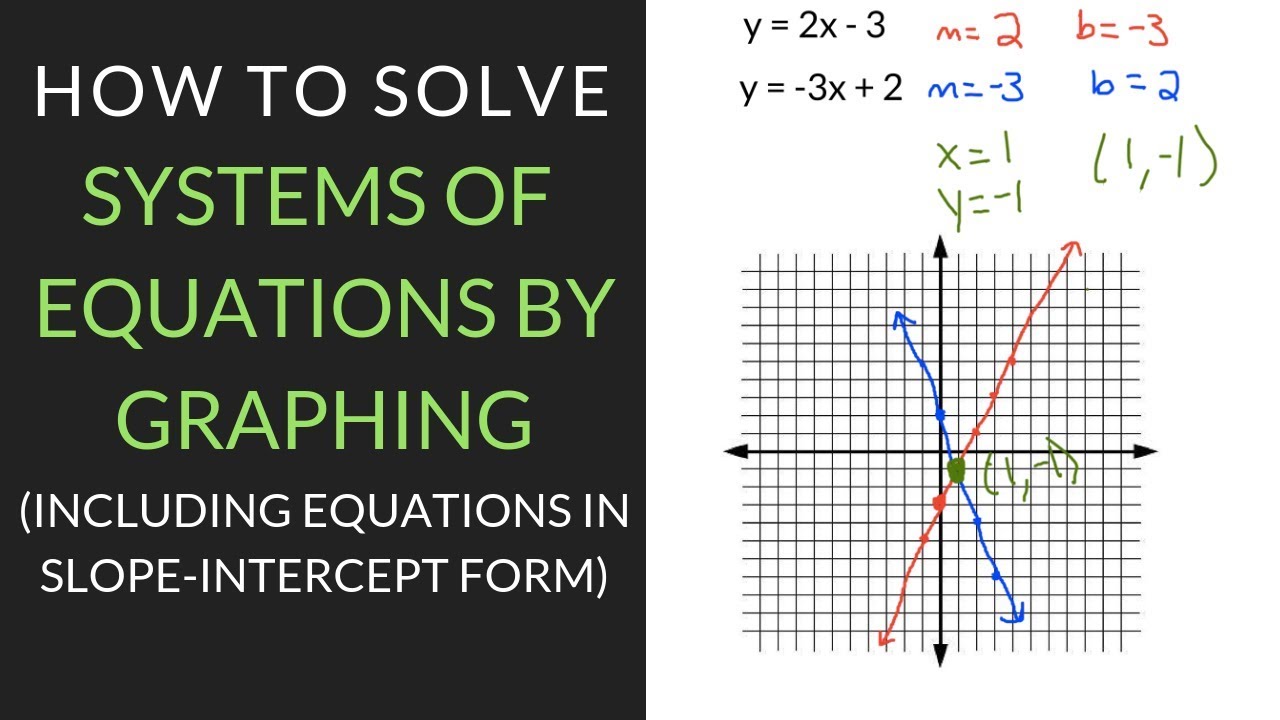
Systems Of Equations Graphs | Kennecott Land

Equations And Inequalities Worksheets | Kennecott Land

Algebra 1 Worksheets Graphing Linear Equations | Kennecott Land

solve system by graphing algebra | Kennecott Land

Solving System Of Equations By Graphing Worksheet Answers | Kennecott Land

Solve Systems By Graphing Worksheets | Kennecott Land
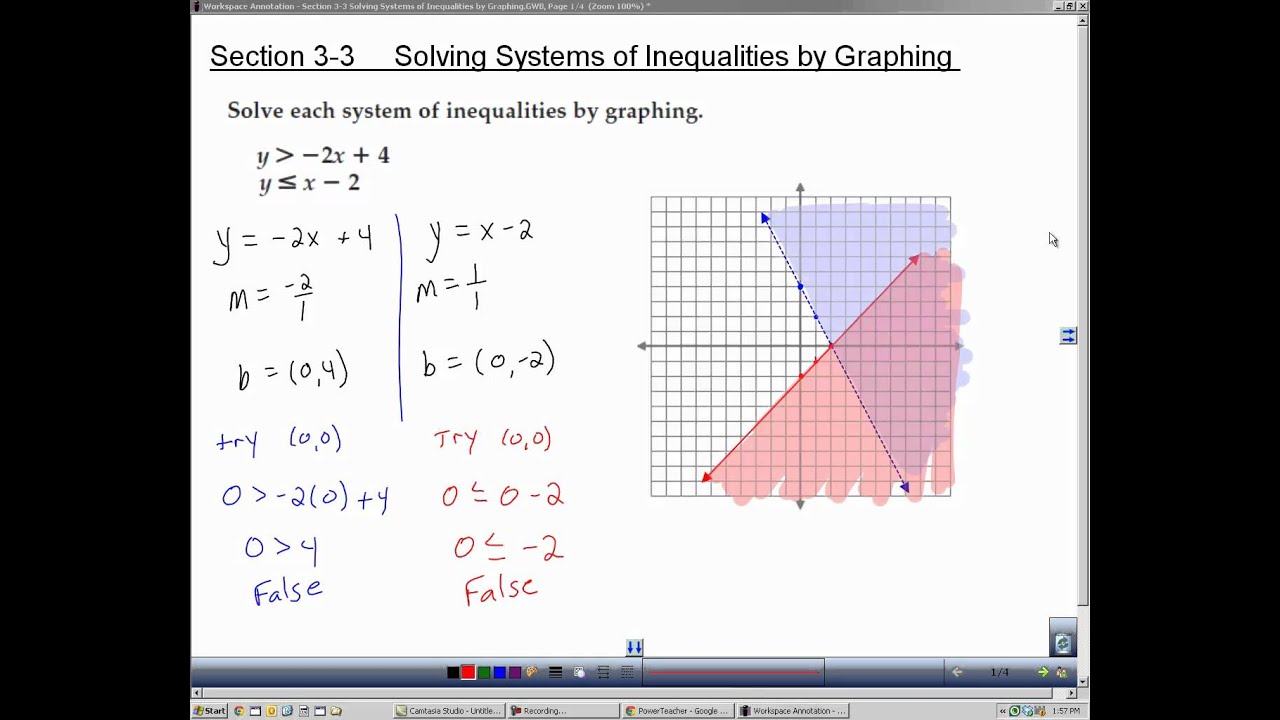
Explain Inequalities In Algebra | Kennecott Land
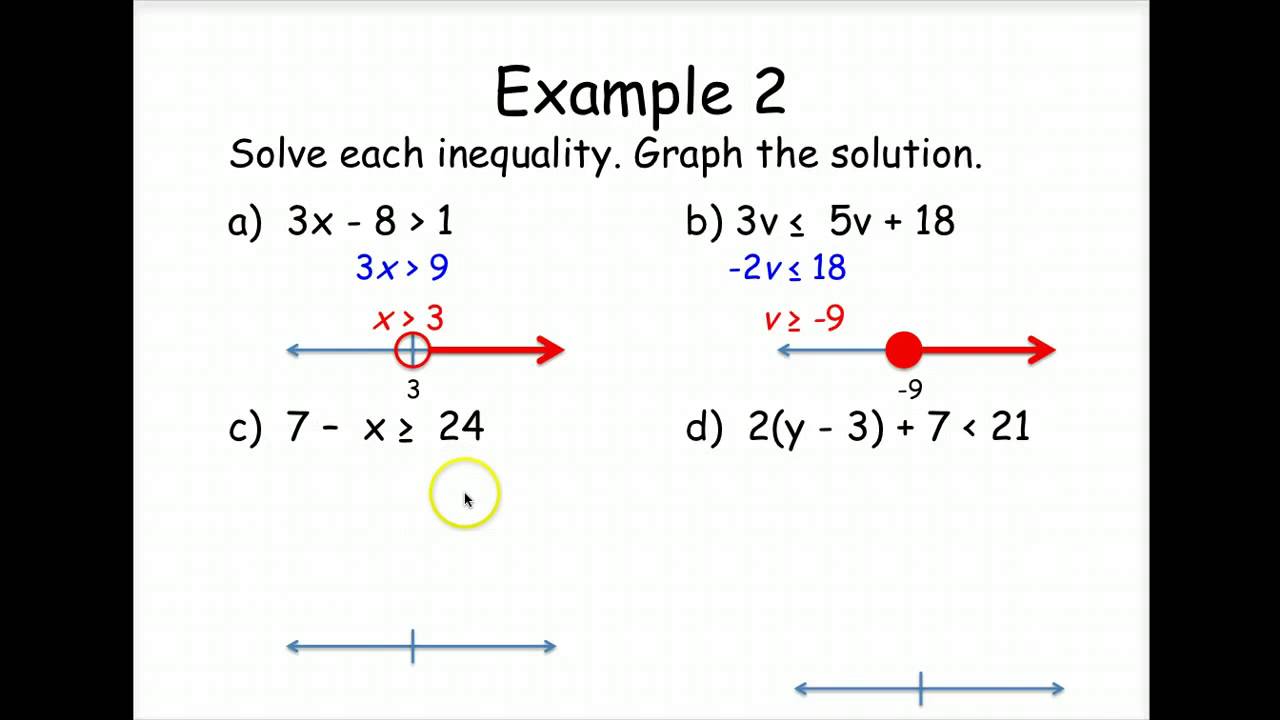
Multi Step Inequalities Infinite Algebra 1 | Kennecott Land