Risolvere un Sistema di Disequazioni Graficamente: Guida Completa
Hai mai avuto bisogno di rappresentare visivamente la soluzione di più disequazioni contemporaneamente? O di trovare l'area comune che soddisfa diverse condizioni matematiche? Se la risposta è sì, allora devi sapere come risolvere un sistema di disequazioni graficamente.
Questa tecnica, fondamentale in algebra, ci permette di visualizzare l'insieme di soluzioni che soddisfano due o più disequazioni. Invece di lavorare solo con numeri, la rappresentazione grafica ci offre un'intuizione immediata della soluzione, rendendo più facile la comprensione del problema e l'individuazione della risposta corretta.
La storia della rappresentazione grafica di sistemi di disequazioni è strettamente legata allo sviluppo della geometria cartesiana, introdotta da René Descartes nel XVII secolo. Questo sistema di coordinate, che tutti conosciamo, ha aperto la strada alla visualizzazione di relazioni matematiche, incluse le disequazioni, rendendo possibile la loro analisi grafica.
Ma a cosa serve, in pratica, risolvere un sistema di disequazioni graficamente? Le applicazioni sono molteplici e spaziano dalla matematica pura all'economia, dalla fisica all'informatica. Ad esempio, potremmo voler ottimizzare la produzione di un'azienda considerando i vincoli di risorse e costi, oppure definire l'area di copertura di un segnale radio tenendo conto di ostacoli e interferenze.
Nonostante la sua utilità, la risoluzione grafica di sistemi di disequazioni può presentare alcune difficoltà. Ad esempio, la precisione del grafico è fondamentale per ottenere una soluzione accurata, e l'interpretazione corretta dell'area di intersezione può essere complessa quando si ha a che fare con molteplici disequazioni. Tuttavia, con la pratica e la conoscenza delle tecniche appropriate, è possibile superare questi ostacoli e utilizzare questo potente strumento matematico con sicurezza.
Vantaggi e Svantaggi della Risoluzione Grafica
| Vantaggi | Svantaggi |
|---|---|
| Visualizzazione immediata della soluzione | Precisione limitata per soluzioni non intere |
| Intuitivo e facile da comprendere | Difficoltà con sistemi di molte disequazioni |
| Utile per problemi di ottimizzazione | Richiede una buona conoscenza delle tecniche di rappresentazione grafica |
Cinque Migliori Pratiche per la Risoluzione Grafica
Ecco cinque consigli utili per aiutarti a risolvere i sistemi di disequazioni graficamente in modo efficace:
- Traccia le rette delle equazioni corrispondenti: Inizia trasformando ogni disequazione in un'equazione. Traccia le rette corrispondenti sul piano cartesiano. Queste rette fungeranno da confini per le regioni che rappresentano le soluzioni delle disequazioni.
- Individua le regioni soluzione: Per ogni disequazione, scegli un punto di prova che non si trovi sulla retta corrispondente. Se il punto di prova soddisfa la disequazione, l'intera regione in cui si trova il punto è parte della soluzione. In caso contrario, la regione opposta alla retta rappresenta la soluzione.
- Evidenzia l'intersezione: L'area dove tutte le regioni soluzione si sovrappongono rappresenta la soluzione del sistema di disequazioni. Evidenzia chiaramente questa area per indicare la soluzione finale.
- Verifica la soluzione: Per essere sicuro di aver risolto correttamente il sistema, scegli un punto all'interno dell'area di intersezione e verifica se soddisfa tutte le disequazioni originali.
- Utilizza strumenti digitali: Esistono diverse applicazioni e siti web che possono aiutarti a rappresentare graficamente sistemi di disequazioni. Questi strumenti possono semplificare il processo e fornire soluzioni più precise.
Domande Frequenti
1. Qual è la differenza tra una disequazione e un'equazione?
Un'equazione stabilisce un'uguaglianza tra due espressioni matematiche, mentre una disequazione esprime una relazione di disuguaglianza (maggiore di, minore di, maggiore o uguale a, minore o uguale a).
2. Cosa significa risolvere un sistema di disequazioni?
Significa trovare l'insieme di tutti i valori che, sostituiti alle incognite, rendono vere tutte le disequazioni del sistema contemporaneamente.
3. Quali sono i metodi alternativi alla risoluzione grafica?
Oltre alla risoluzione grafica, è possibile risolvere un sistema di disequazioni utilizzando metodi algebrici, come il metodo di sostituzione o il metodo di eliminazione.
4. Posso risolvere sistemi di disequazioni con più di due variabili graficamente?
La rappresentazione grafica diventa più complessa all'aumentare del numero di variabili. Per sistemi con più di due variabili, si ricorre a metodi algebrici o a software di calcolo.
5. Quali sono le applicazioni pratiche della risoluzione di sistemi di disequazioni?
Le applicazioni sono numerose e spaziano dall'economia (ottimizzazione dei profitti), all'ingegneria (progettazione di strutture), alla fisica (studio del moto di oggetti soggetti a vincoli).
6. Qual è la differenza tra una retta tratteggiata e una retta continua nel grafico di una disequazione?
Una retta continua indica che i punti sulla retta sono inclusi nella soluzione (≥ o ≤), mentre una retta tratteggiata indica che i punti sulla retta non sono inclusi (< o >).
7. Come si rappresenta graficamente una disequazione con il simbolo "maggiore di" (>) o "minore di" (<)?
Si utilizza una retta tratteggiata per rappresentare il confine della regione soluzione. L'area sopra la retta rappresenta la soluzione per "maggiore di", mentre l'area sotto la retta rappresenta la soluzione per "minore di".
8. Come posso migliorare le mie capacità di risoluzione di sistemi di disequazioni?
La pratica costante è fondamentale. Esercitati con diversi esempi, utilizza strumenti digitali per la visualizzazione e consulta risorse online o testi scolastici per approfondire la tua comprensione.
In conclusione, risolvere un sistema di disequazioni graficamente è una tecnica potente e versatile che trova applicazione in molteplici ambiti. Sebbene presenti alcune sfide, la padronanza di questa tecnica offre una profonda comprensione delle relazioni tra le disequazioni e permette di visualizzare e interpretare le soluzioni in modo intuitivo. Attraverso la pratica costante e l'utilizzo di strategie efficaci, potrai risolvere con successo sistemi di disequazioni e utilizzare questo strumento matematico a tuo vantaggio.

Graphing Inequalities On A Coordinate Plane Worksheets | Kennecott Land

Solving Systems By Graphing Worksheets Algebra 2 | Kennecott Land
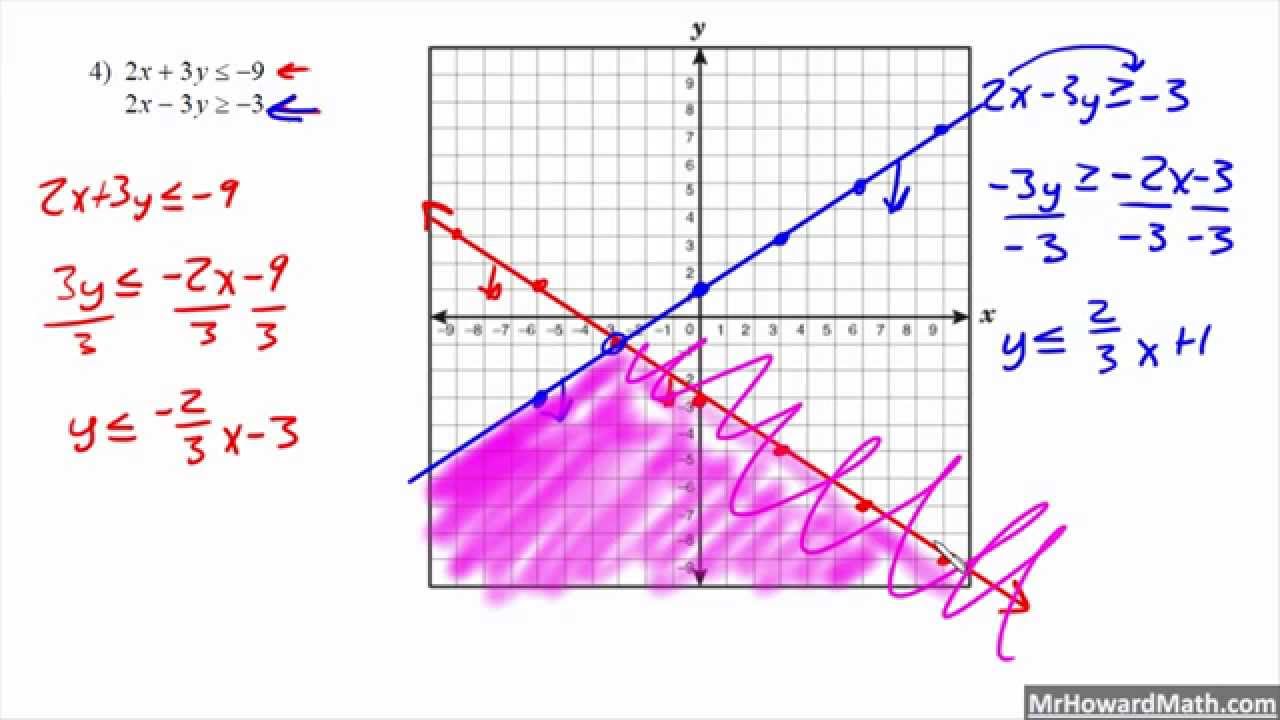
System Of Inequalities How To Solve | Kennecott Land

Equations And Inequalities Practice Pdf | Kennecott Land

This System Of Linear Inequalities Examples | Kennecott Land

Solve And Graph Linear Inequalities Worksheet | Kennecott Land

Linear Equations And Inequalities Examples | Kennecott Land

Solve Compound Inequalities Worksheet | Kennecott Land
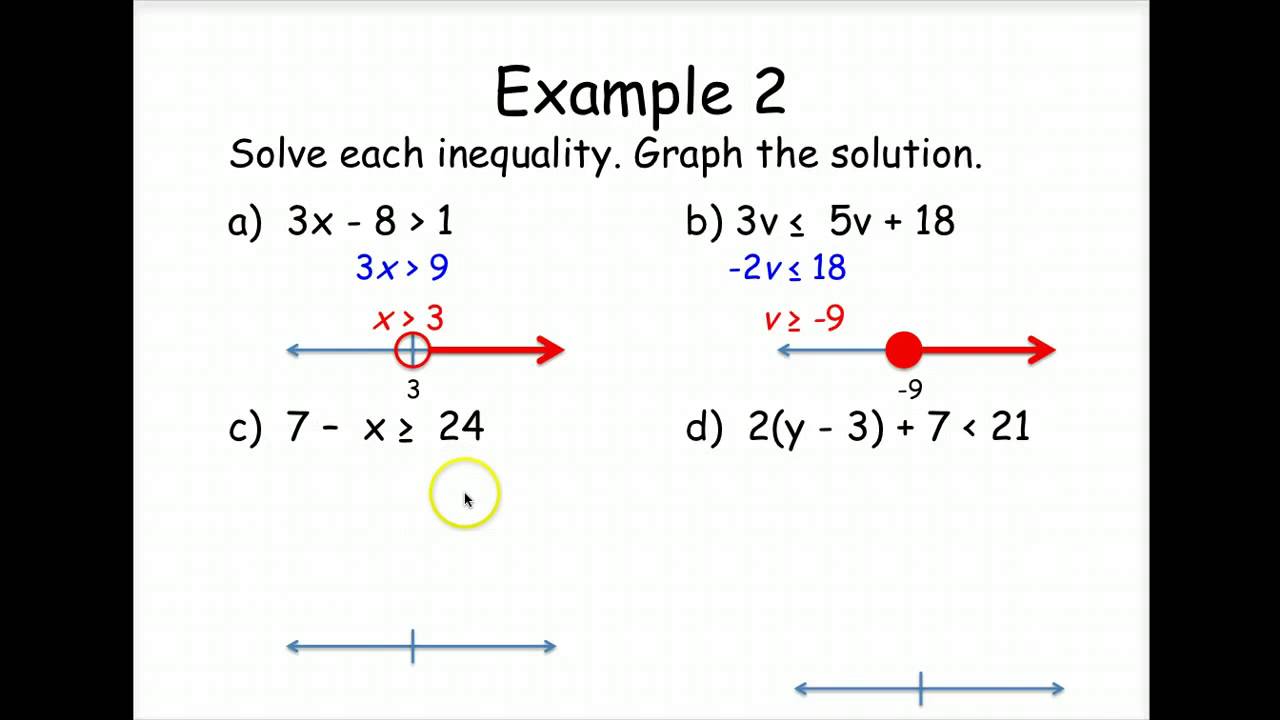
Math Equations And Inequalities | Kennecott Land

System Of Inequalities Explained | Kennecott Land
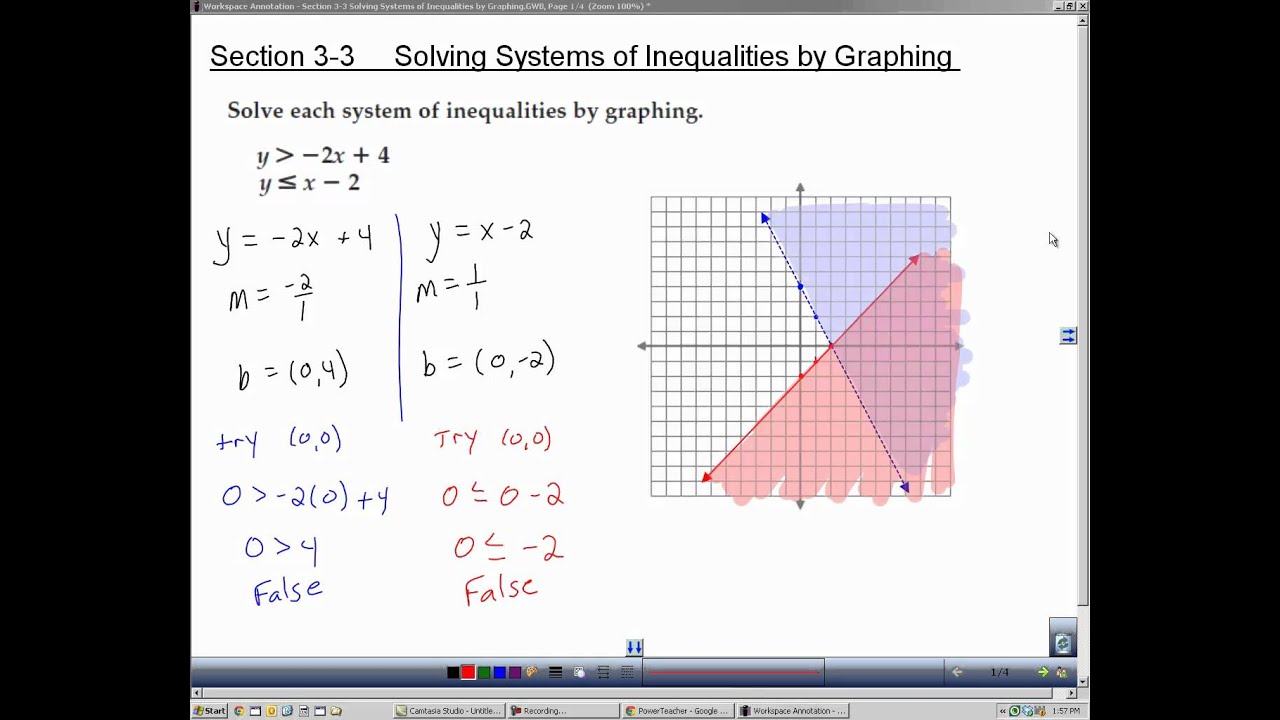
Explain Inequalities In Algebra | Kennecott Land

Equations And Inequalities Algebra 1 | Kennecott Land

System Of Linear Inequalities Example | Kennecott Land

Graphing Systems of Inequalities in 3 Easy Steps | Kennecott Land

7.6 systems of inequalities worksheet | Kennecott Land