Simbol Ajaib: Rahsia 'Dan' & 'Atau' Dalam Matematik
Pernah tak korang terfikir, macam mana ahli matematik boleh selesaikan masalah yang kompleks dengan hanya beberapa simbol? Macam ada bahasa rahsia je kan? Sebenarnya, simbol-simbol dalam matematik ni macam kod rahsia yang bantu kita faham konsep matematik dengan lebih mudah. Dua daripada simbol yang paling penting dan selalu kita jumpa ialah 'dan' dan 'atau'.
Walaupun nampak simple, tapi jangan pandang rendah pada kuasa simbol 'dan' dan 'atau' ni. Dalam dunia matematik, simbol-simbol ni memainkan peranan yang sangat penting untuk menghubungkan idea, membentuk pernyataan logik, dan menyelesaikan pelbagai masalah. Korang bayangkanlah macam mana huru-hara dunia matematik kalau takde simbol-simbol ni.
Simbol 'dan' biasanya diwakili oleh simbol '∧' atau '&', manakala simbol 'atau' diwakili oleh simbol '∨'. Dalam kehidupan seharian, kita guna perkataan 'dan' dan 'atau' untuk menghubungkan ayat. Tapi dalam matematik, simbol-simbol ni bukan sekadar penghubung ayat, tapi ada makna yang lebih spesifik dan tepat.
Sebagai contoh, cuba bayangkan korang nak beli aiskrim. Korang nak aiskrim coklat 'dan' vanila. Maksudnya, korang mesti dapat kedua-dua perisa tu baru lengkap. Tapi kalau korang cakap nak aiskrim coklat 'atau' vanila, maksudnya korang okay je dapat salah satu perisa, tak kisahlah coklat atau vanila. Nampak tak perbezaan penggunaan 'dan' dan 'atau' dalam konteks ni?
Konsep 'dan' dan 'atau' ni bukan benda baru, malah dah wujud sejak zaman Greek kuno lagi! Ahli falsafah dan ahli matematik zaman tu dah mula kaji konsep logik dan guna simbol untuk wakili idea-idea ni. Seiring dengan peredaran masa, simbol-simbol ni terus berkembang dan digunakan secara meluas dalam pelbagai bidang, termasuklah sains komputer, kejuruteraan, dan statistik.
Kelebihan dan Kekurangan Simbol 'Dan' & 'Atau'
Penggunaan simbol 'dan' dan 'atau' dalam matematik, seperti banyak konsep lain, hadir dengan kelebihan dan kekurangannya sendiri. Berikut adalah gambaran ringkas:
| Aspek | Kelebihan | Kekurangan |
|---|---|---|
| Kejelasan | Membuat pernyataan matematik lebih ringkas dan tepat. | Boleh menyebabkan kekeliruan jika tidak difahami dengan betul. |
| Kecekapan | Membolehkan manipulasi logik yang kompleks dengan mudah. | Penggunaan yang salah boleh membawa kepada kesimpulan yang salah. |
| Aplikasi Luas | Digunakan dalam pelbagai bidang matematik dan sains komputer. | Pengetahuan tentang simbol lain dan peraturan logik diperlukan untuk aplikasi yang lebih kompleks. |
Walaupun terdapat kekurangan, kelebihan penggunaan simbol 'dan' dan 'atau' dalam matematik jauh mengatasi keburukannya. Dengan pemahaman yang jelas tentang konsep ini, kita dapat membuka kunci kepada pemahaman yang lebih mendalam tentang matematik dan logik.
Secara ringkasnya, simbol 'dan' dan 'atau' adalah elemen penting dalam bahasa matematik. Walaupun nampak ringkas, simbol-simbol ni memainkan peranan yang besar dalam membantu kita memahami dan menyelesaikan masalah matematik. Jadi, jangan pandang rendah pada kuasa simbol-simbol kecil ni, okay?

Apa Itu Matematika Diskrit | Kennecott Land

Detail Lambang Lambang Dalam Matematika Koleksi Nomer 8 | Kennecott Land
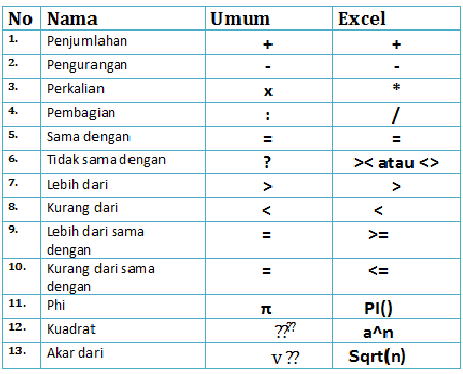
simbol dan atau dalam matematika | Kennecott Land

simbol dan atau dalam matematika | Kennecott Land

Apa Arti Dalam Matematika | Kennecott Land

Simbol Simbol Matematika Lengkap | Kennecott Land
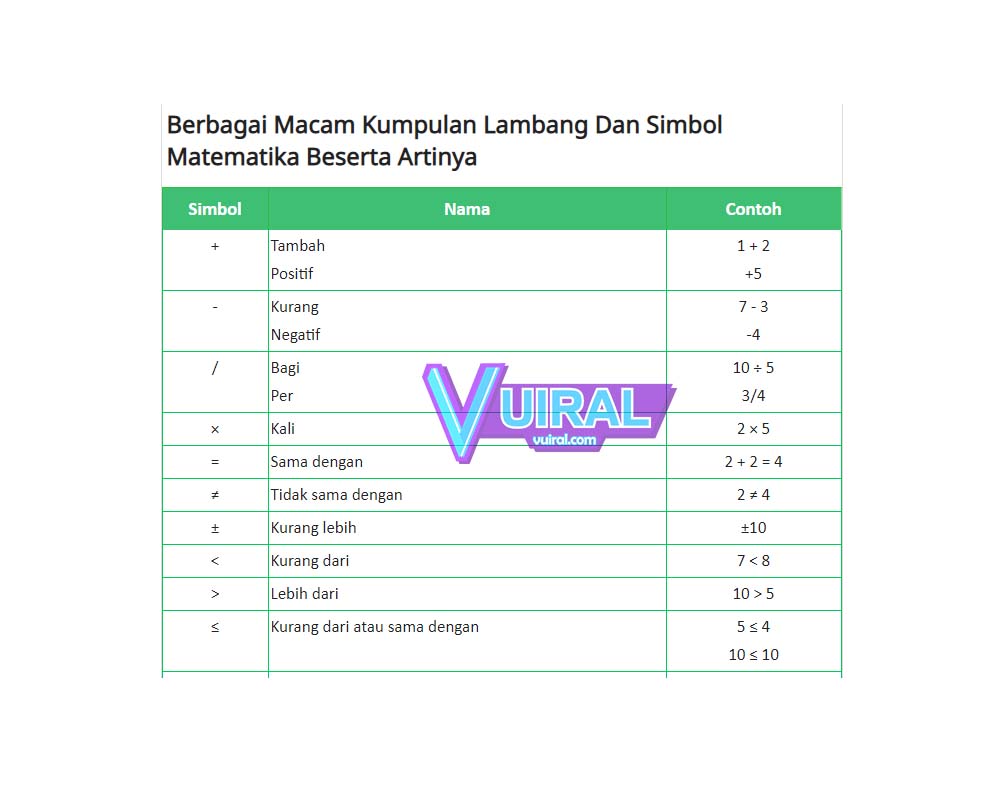
Arti Simbol Dalam Matematika | Kennecott Land

Tanda Lebih Besar Dan Lebih Kecil Dalam Matematika | Kennecott Land
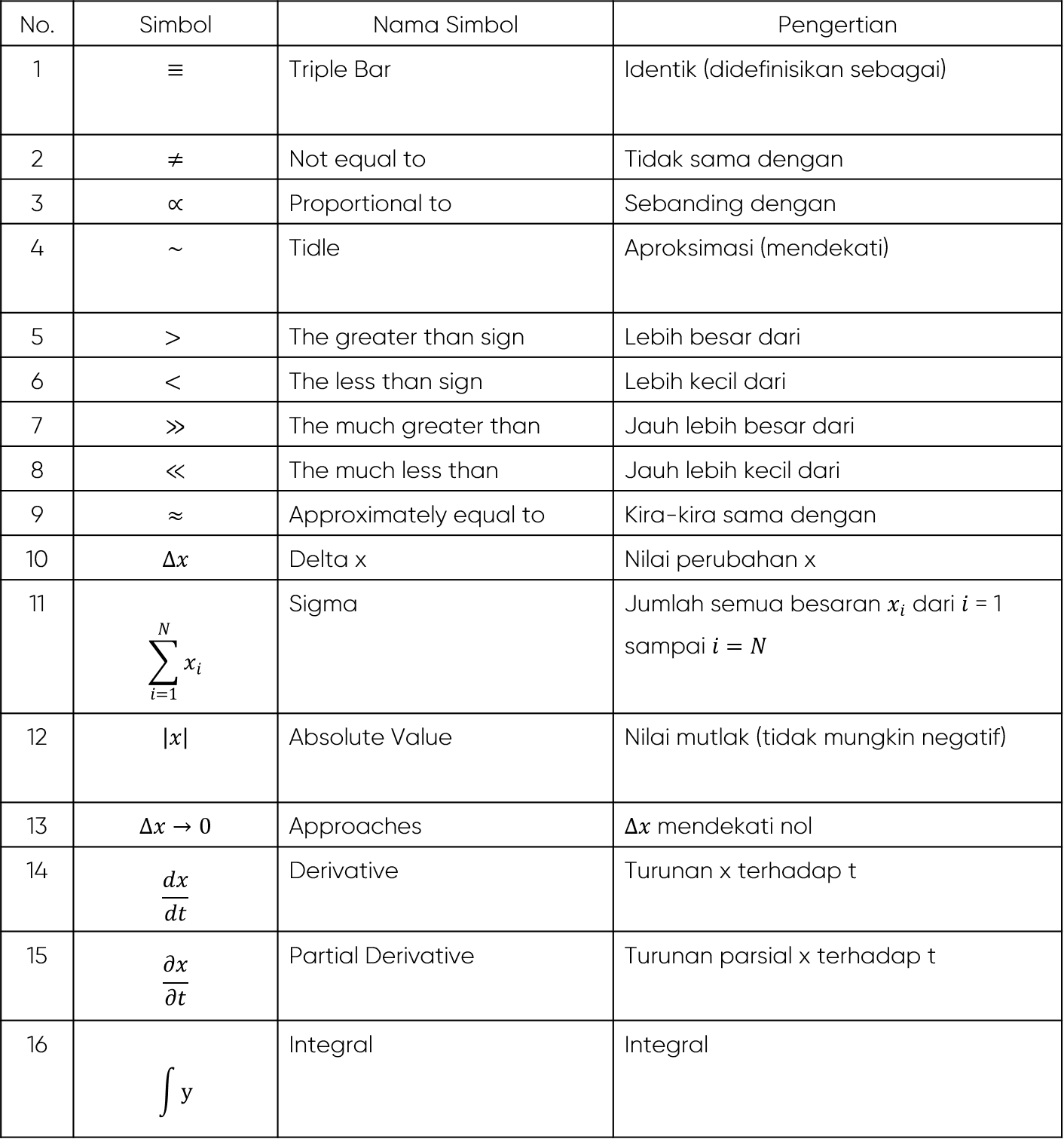
Penggunaan Simbol Matematika pada Fisika Beserta Pengertiannya | Kennecott Land

simbol dan atau dalam matematika | Kennecott Land