Simbol dan 'Pada' dalam Matematik: Bahasa Universal Nombor
Pernahkah anda terfikir bagaimana bahasa matematik difahami di seluruh dunia walaupun dengan perbezaan bahasa dan budaya? Jawapannya terletak pada simbol dan 'pada' yang membentuk bahasa universal matematik. Simbol seperti +, -, ×, ÷, =, dan banyak lagi, membolehkan kita meluahkan konsep matematik dengan ringkas dan tepat.
Simbol dalam matematik bertindak sebagai singkatan idea yang kompleks, menjadikan komunikasi idea matematik lebih mudah dan efisien. Bayangkan cuba menyatakan persamaan Pythagoras menggunakan perkataan sahaja - ia akan menjadi rumit dan sukar difahami! Dengan simbol, persamaan itu menjadi ringkas: a² + b² = c².
Penggunaan simbol dalam matematik bermula sejak zaman purba. Orang Babylon menggunakan sistem nombor berasaskan 60 dan simbol untuk mewakili nombor dan operasi. Orang Mesir purba pula menggunakan hieroglif untuk mewakili nombor dan konsep matematik. Simbol-simbol ini berkembang dari masa ke masa, dipengaruhi oleh pelbagai budaya dan ahli matematik. Tokoh-tokoh penting seperti Diophantus, Brahmagupta, dan al-Khwarizmi telah memberi sumbangan besar kepada perkembangan simbol matematik yang kita gunakan hari ini.
Simbol 'pada' dalam matematik juga penting. Ia digunakan untuk menunjukkan hubungan antara kuantiti dalam pelbagai konteks, seperti nisbah, kadar, dan perkadaran. Sebagai contoh, "3 pada 5" boleh mewakili nisbah antara 3 bahagian dan 5 bahagian. Memahami konsep 'pada' adalah penting dalam pelbagai bidang matematik, termasuk algebra, kalkulus dan statistik.
Kepentingan simbol dan 'pada' dalam matematik tidak boleh dipertikaikan. Mereka membolehkan komunikasi yang tepat dan efisien, memudahkan penyelesaian masalah, dan membuka jalan kepada penemuan dan inovasi baru dalam bidang matematik. Tanpa simbol dan 'pada', matematik akan menjadi bahasa yang rumit dan tidak praktikal.
Salah satu manfaat utama simbol dan 'pada' dalam matematik adalah ketepatan mereka. Simbol matematik mempunyai makna yang jelas dan tepat, menghapuskan sebarang kekaburan atau salah tafsir. Contohnya, simbol '=' bermaksud "sama dengan" dan tidak boleh digunakan untuk mewakili apa-apa yang lain. Ketepatan ini penting dalam memastikan ketelitian dan kebolehpercayaan dalam pengiraan dan penaakulan matematik.
Simbol dan 'pada' juga membolehkan kita bekerja dengan konsep matematik yang abstrak dan kompleks dengan lebih mudah. Mereka menyediakan cara untuk mewakilkan dan memanipulasi idea matematik yang tidak dapat diungkapkan dengan mudah menggunakan perkataan sahaja. Contohnya, simbol '∞' mewakili konsep infiniti, yang sukar difahami tanpa simbol.
Penggunaan simbol dan 'pada' juga menjadikan matematik lebih mudah diakses oleh orang dari pelbagai latar belakang budaya dan bahasa. Simbol matematik adalah bahasa universal, mengatasi halangan linguistik dan memudahkan kolaborasi dan perkongsian pengetahuan dalam komuniti matematik global.
Kelebihan dan Kekurangan Simbol dan 'Pada' dalam Matematik
| Kelebihan | Kekurangan |
|---|---|
| Ketepatan dan kejelasan | Simbol boleh menjadi sukar untuk dipelajari dan diingat |
| Komunikasi yang efisien | Penggunaan simbol yang berlebihan boleh menjadikan matematik kelihatan abstrak dan tidak dapat didekati |
| Memudahkan penyelesaian masalah | Simbol boleh disalahgunakan dan membawa kepada kesimpulan yang salah |
| Aksesibiliti global |
Berikut adalah beberapa amalan terbaik untuk melaksanakan simbol dan 'pada' dalam matematik:
- Ketahui makna setiap simbol. Sebelum menggunakan simbol, pastikan anda memahami maknanya dan bagaimana ia digunakan dalam konteks matematik.
- Gunakan simbol dengan konsisten. Jangan gunakan simbol yang berbeza untuk mewakili konsep yang sama.
- Gunakan simbol dengan teliti. Pastikan simbol yang anda gunakan sesuai untuk konteksnya dan tidak menimbulkan kekaburan.
- Terangkan penggunaan simbol. Apabila memperkenalkan simbol baru kepada pelajar atau pembaca, terangkan maknanya dan bagaimana ia digunakan.
- Latih penggunaan simbol. Amalkan menyelesaikan masalah dan menulis ungkapan matematik menggunakan simbol untuk mengukuhkan pemahaman anda.
Berikut adalah beberapa contoh cabaran dan penyelesaian berkaitan simbol dan 'pada' dalam matematik:
- Cabaran: Pelajar keliru dengan simbol yang serupa, seperti '+' dan '×'. Penyelesaian: Tekankan perbezaan antara simbol dan maknanya. Gunakan bantuan visual dan aktiviti hands-on untuk mengukuhkan pemahaman.
- Cabaran: Pelajar sukar memahami konsep 'pada' dalam nisbah dan perkadaran. Penyelesaian: Gunakan contoh konkrit dan objek manipulatif untuk menggambarkan konsep 'pada'. Hubungkan konsep 'pada' dengan situasi kehidupan sebenar.
- Cabaran: Pelajar terlupa makna simbol. Penyelesaian: Gunakan carta rujukan dan permainan matematik untuk membantu pelajar mengingat makna simbol.
- Cabaran: Pelajar menggunakan simbol secara tidak betul. Penyelesaian: Berikan maklum balas yang kerap dan pembetulan kesilapan. Tekankan pentingnya penggunaan simbol yang betul.
- Cabaran: Pelajar takut menggunakan simbol dalam matematik. Penyelesaian: Cipta persekitaran pembelajaran yang positif dan menggalakkan. Galakkan pelajar untuk bertanya soalan dan mengambil risiko.
Berikut adalah beberapa soalan lazim berkaitan simbol dan 'pada' dalam matematik:
- Apakah simbol yang paling penting dalam matematik?
Tidak ada satu simbol yang paling penting, tetapi beberapa simbol yang paling asas dan kerap digunakan termasuk +, -, ×, ÷, =, <, >, dan √.
- Bagaimana saya boleh belajar mengingati semua simbol matematik?
Amalan dan pengulangan adalah kunci untuk mengingati simbol matematik. Gunakan kad imbas, carta rujukan dan permainan matematik untuk membantu anda mempelajari dan mengingati simbol.
- Adakah simbol matematik sentiasa sama di seluruh dunia?
Walaupun kebanyakan simbol matematik adalah universal, terdapat beberapa variasi kecil dalam beberapa budaya dan negara. Contohnya, simbol perpuluhan boleh ditulis sebagai titik (.) di beberapa negara dan koma (,) di negara lain.
- Apakah sejarah di sebalik simbol 'pada'?
Simbol 'pada' (/) mempunyai sejarah yang panjang dan telah digunakan dalam pelbagai konteks. Dalam matematik, ia mula digunakan untuk mewakili nisbah pada abad ke-17. Simbol ini mungkin berasal dari perkataan Latin "per", yang bermaksud "oleh" atau "untuk".
- Bagaimana saya boleh meningkatkan kemahiran saya dalam menggunakan simbol dan 'pada' dalam matematik?
Latih tubi secara konsisten, dapatkan maklum balas daripada guru atau tutor, dan terokai sumber pembelajaran tambahan, seperti buku teks, laman web dan aplikasi matematik.
- Apakah sumber yang baik untuk belajar tentang simbol dan 'pada' dalam matematik?
Beberapa sumber yang baik termasuk:
- Buku teks matematik
- Laman web seperti Khan Academy dan Math is Fun
- Aplikasi matematik seperti Photomath dan Wolfram Alpha
Tips dan trik untuk menguasai simbol dan 'pada' dalam matematik:
- Buat nota ringkas. Tulis simbol, maknanya, dan contoh penggunaannya dalam buku nota atau kad imbas.
- Latih tubi secara berkala. Selesaikan pelbagai masalah matematik yang melibatkan simbol dan 'pada'.
- Gunakan bantuan visual. Gunakan gambar rajah, graf, dan objek manipulatif untuk membantu anda memahami konsep.
- Berbincang dengan rakan sebaya. Bincangkan konsep matematik dan selesaikan masalah bersama-sama.
- Cari corak. Cari corak dalam penggunaan simbol dan 'pada' untuk membantu anda mengingati dan memahaminya.
Kesimpulannya, simbol dan 'pada' adalah komponen penting dalam bahasa matematik. Mereka membolehkan komunikasi yang tepat dan efisien, memudahkan penyelesaian masalah, dan membuka jalan kepada penemuan dan inovasi baru. Dengan memahami kepentingan, sejarah, dan aplikasi praktikal simbol dan 'pada', kita dapat meningkatkan pemahaman kita tentang matematik dan menghargai keindahan dan kuasa bahasa universal ini. Marilah kita terus meneroka dan menguasai simbol dan 'pada' dalam matematik untuk membuka kunci potensi penuh pemikiran matematik dan meneroka keajaiban dunia di sekeliling kita.
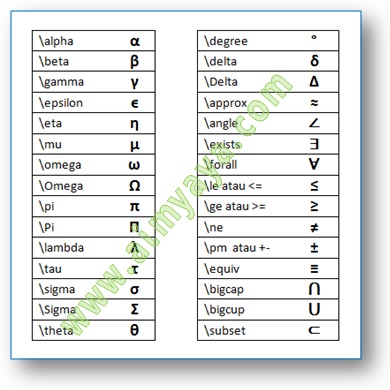
How to put sigma symbol in word | Kennecott Land
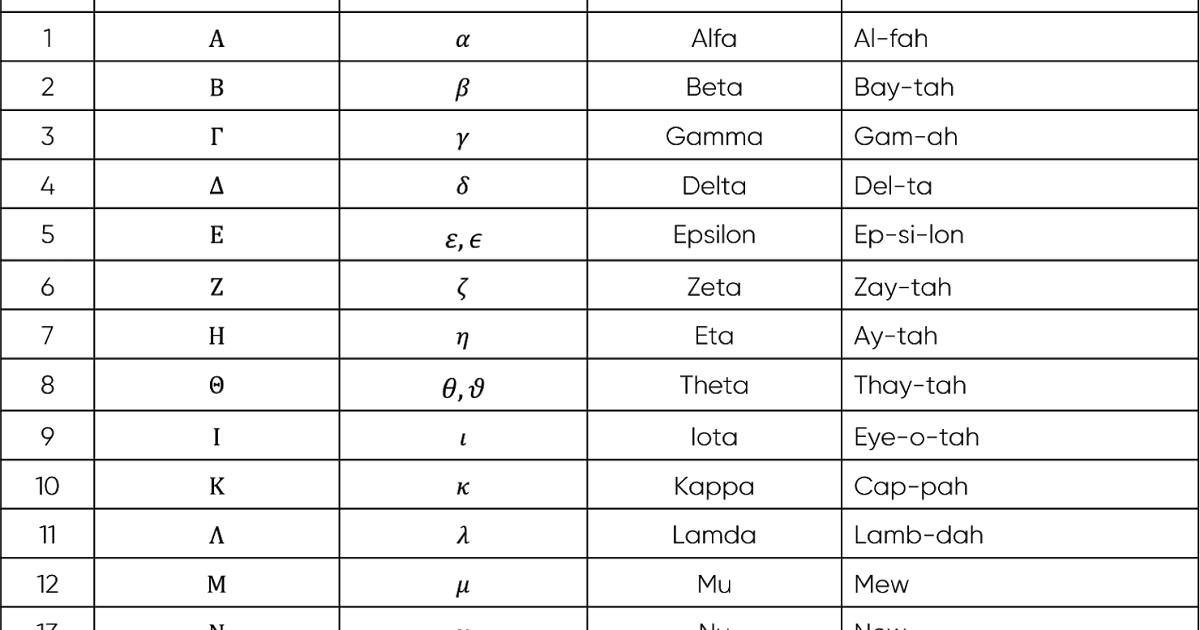
Penggunaan Huruf Yunani (Greece) pada Fisika Beserta Pengucapannya | Kennecott Land

Simbol Simbol Matematika Lengkap | Kennecott Land
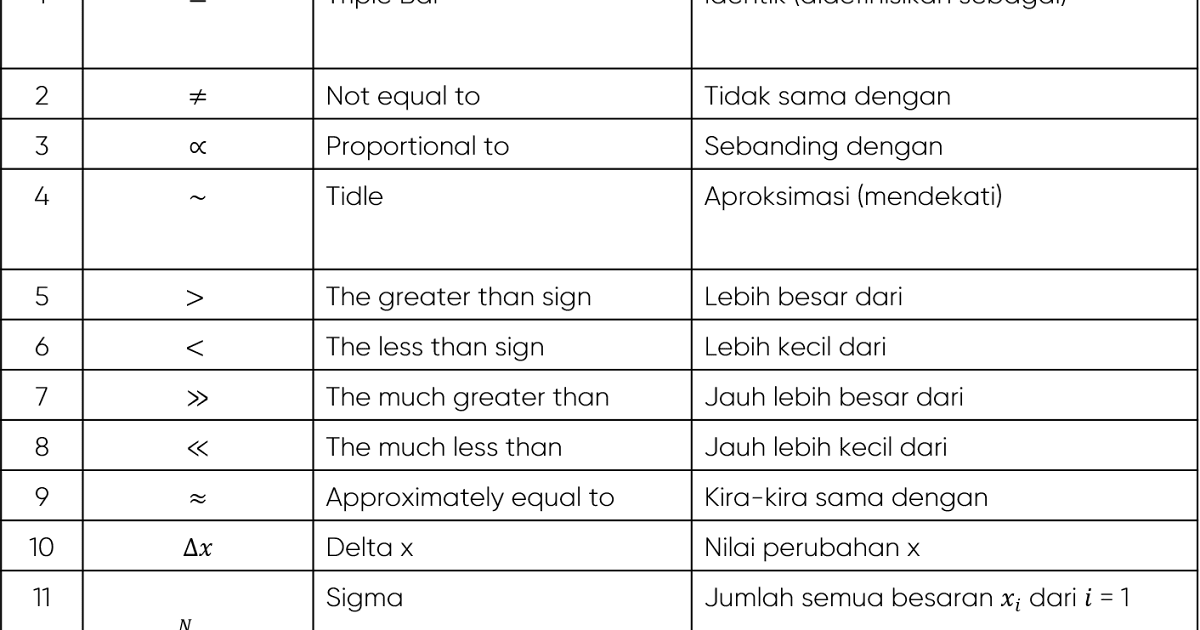
Notasi Matematika Dan Artinya | Kennecott Land

simbol dan pada matematika | Kennecott Land
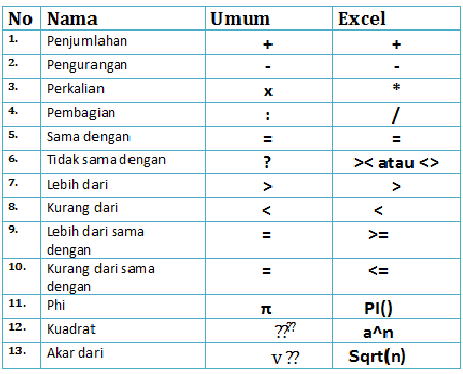
simbol dan pada matematika | Kennecott Land

Penggunaan Simbol Matematika pada Fisika Beserta Pengertiannya | Kennecott Land

Arti Delta Dalam Matematika | Kennecott Land