De ln(x)=4 Vergelijking Oplossen: Een Praktische Gids
De wereld van de wiskunde zit vol met fascinerende vergelijkingen en functies die ons helpen de wereld om ons heen te begrijpen. Een van die intrigerende concepten is de natuurlijke logaritme, vaak afgekort als "ln". In deze gids duiken we in de wereld van logaritmen en onderzoeken we hoe we de vergelijking ln(x) = 4 kunnen oplossen.
Stel je voor dat je te maken krijgt met een probleem waarbij een onbekende variabele vastzit in een natuurlijke logaritme. Hoe bevrijd je de onbekende en vind je de oplossing? Dat is precies wat we hier zullen ontdekken. We zullen de stappen doornemen die nodig zijn om ln(x) = 4 op te lossen, en we zullen de onderliggende principes verkennen die deze wiskundige puzzel aandrijven.
Logaritmen, en in het bijzonder natuurlijke logaritmen, spelen een cruciale rol in verschillende wetenschappelijke disciplines. Ze worden gebruikt in de natuurkunde om exponentiële groei en verval te modelleren, in de scheikunde om de pH van oplossingen te berekenen, en in de financiële wereld om rentegroei te analyseren. Door de ln(x) = 4 vergelijking te begrijpen en op te lossen, open je de deur naar een beter begrip van deze toepassingen in de echte wereld.
Voordat we in de details van het oplossen duiken, laten we eerst de basisprincipes van natuurlijke logaritmen vaststellen. De natuurlijke logaritme van een getal is de exponent waartoe je het getal e (de wiskundige constante ongeveer gelijk aan 2,718) moet verheffen om dat getal te krijgen. Met andere woorden, als ln(x) = y, dan is e^y = x.
Gewapend met deze kennis, kunnen we nu de stappen aanpakken om de vergelijking ln(x) = 4 op te lossen. Het doel is om x te isoleren, en we kunnen dit doen door gebruik te maken van de inverse bewerking van de natuurlijke logaritme, namelijk de exponentiële functie met grondtal e. Door beide zijden van de vergelijking te verheffen tot de macht e, krijgen we:
e^(ln(x)) = e^4
Omdat de exponentiële functie met grondtal e en de natuurlijke logaritme inverse bewerkingen van elkaar zijn, heffen ze elkaar op, waardoor we x alleen overhouden:
x = e^4
Met een rekenmachine kunnen we e^4 berekenen, wat ongeveer gelijk is aan 54,598. Dus de oplossing van de vergelijking ln(x) = 4 is x = 54,598.
Voor- en nadelen van het begrijpen van ln(x) = 4
| Voordelen | Nadelen |
|---|---|
| Essentieel voor verschillende wetenschappelijke disciplines | Vereist kennis van logaritmen en exponentiële functies |
| Helpt bij het oplossen van praktische problemen in de natuurkunde, scheikunde en financiën | Kan voor beginners uitdagend lijken |
| Verbetert het probleemoplossend vermogen | - |
Het begrijpen en kunnen oplossen van logaritmische vergelijkingen zoals ln(x) = 4 opent de deur naar een dieper begrip van wiskundige concepten en hun toepassingen in de echte wereld. Hoewel het in het begin misschien uitdagend lijkt, zijn de beloningen van het beheersen van deze vaardigheid talrijk.

how to solve ln x 4 | Kennecott Land

how to solve ln x 4 | Kennecott Land

how to solve ln x 4 | Kennecott Land
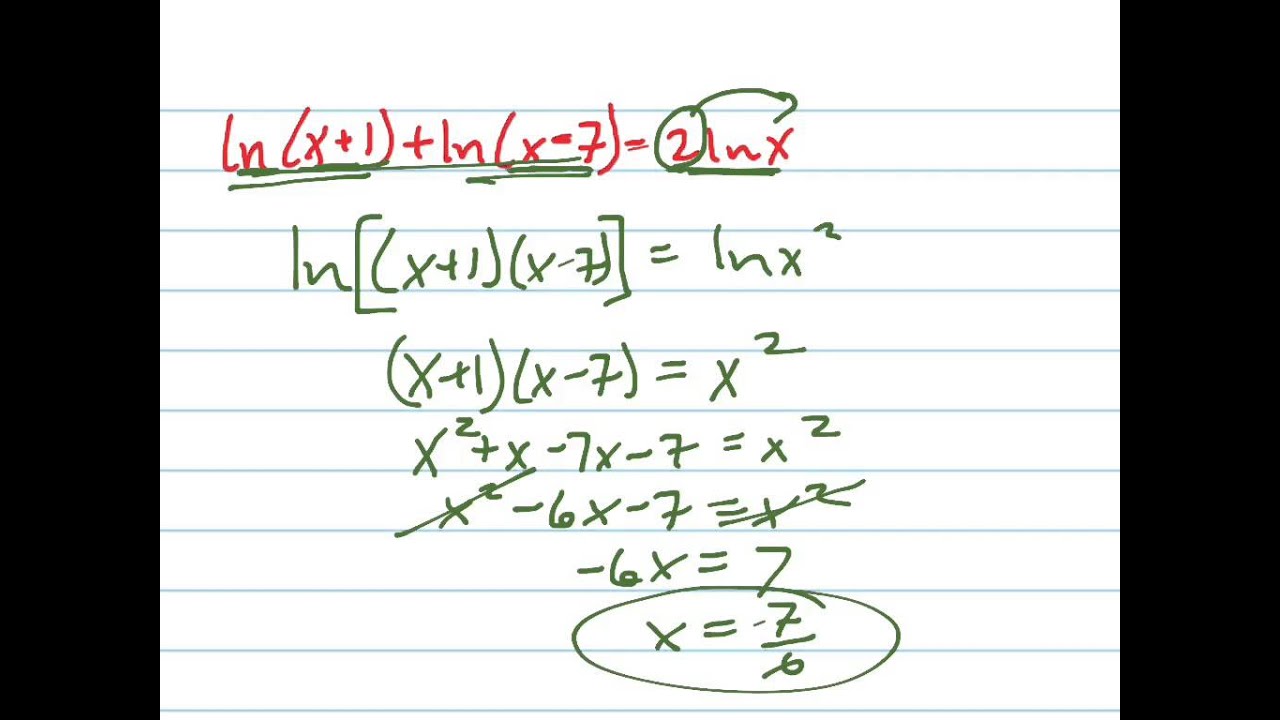
how to solve ln x 4 | Kennecott Land

how to solve ln x 4 | Kennecott Land

how to solve ln x 4 | Kennecott Land

how to solve ln x 4 | Kennecott Land

Question Video: Using Logarithmic Differentiation to Differentiate a | Kennecott Land

how to solve ln x 4 | Kennecott Land

how to solve ln x 4 | Kennecott Land
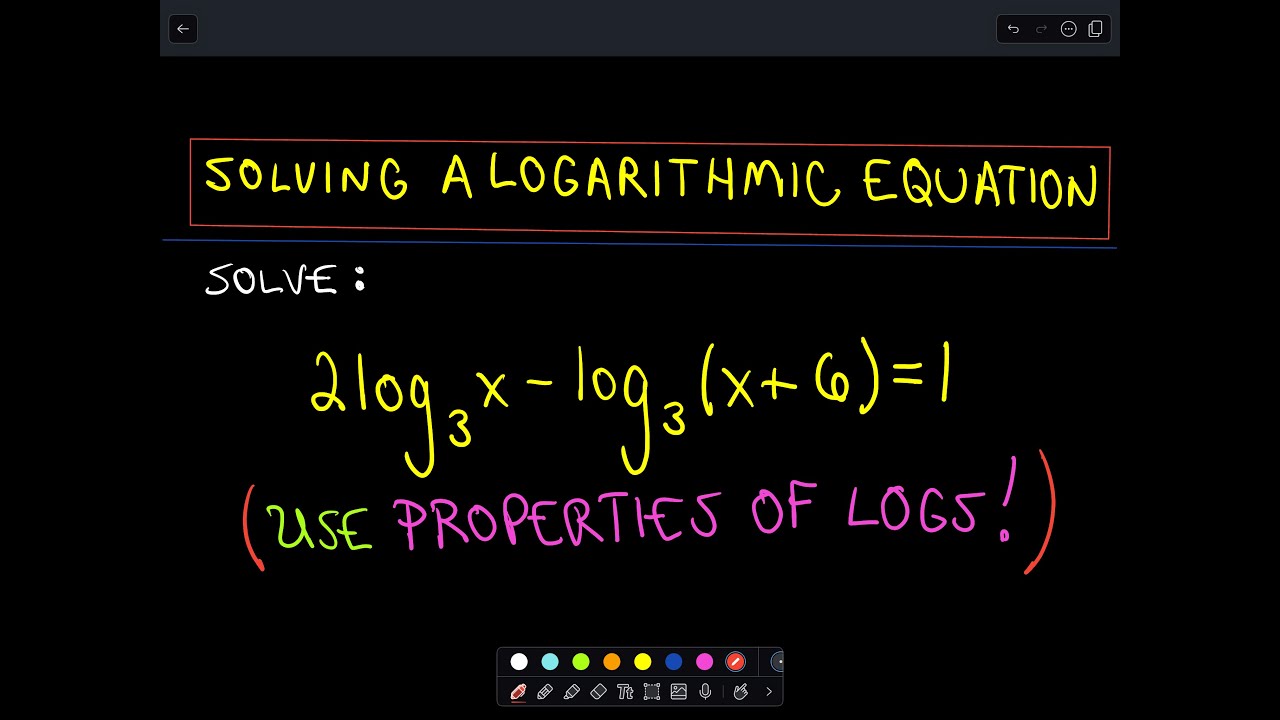
Logarithmic Equations Examples And Solutions | Kennecott Land

how to solve ln x 4 | Kennecott Land

how to solve ln x 4 | Kennecott Land

how to solve ln x 4 | Kennecott Land

how to solve ln x 4 | Kennecott Land