De Magie van Regressiecoëfficiënten Ontrafeld: Begrijp de Kracht van Data
Wat schuilt er achter de cijfers? Hoe ontrafelen we de verborgen relaties in data? Het antwoord ligt in de fascinerende wereld van regressiecoëfficiënten. Deze ogenschijnlijk eenvoudige getallen bevatten een schat aan informatie en vormen de sleutel tot het begrijpen van complexe verbanden. In dit artikel duiken we diep in de wereld van regressiecoëfficiënten, ontrafelen hun betekenis en verkennen hoe ze ons helpen om data om te zetten in waardevolle inzichten.
Stel je voor dat je de impact van reclame-uitgaven op de verkoop wilt meten. Of de relatie tussen temperatuur en ijsconsumptie. Regressiecoëfficiënten zijn de magische getallen die je hierbij helpen. Ze kwantificeren de invloed van één variabele op een andere, en bieden daarmee een krachtige tool voor data-analyse en voorspellingen.
Een regressiecoëfficiënt, wat is dat nu precies? In essentie is het een numerieke waarde die de verandering in de afhankelijke variabele (bijvoorbeeld verkoop) weergeeft voor elke eenheidsverandering in de onafhankelijke variabele (bijvoorbeeld reclame-uitgaven), terwijl alle andere variabelen constant worden gehouden. Het is de helling van de regressielijn, die de relatie tussen de variabelen visualiseert.
Het concept van regressiecoëfficiënten vindt zijn oorsprong in het werk van Sir Francis Galton in de 19e eeuw. Galton bestudeerde de relatie tussen de lengte van ouders en hun kinderen en ontdekte een lineair verband. Deze ontdekking legde de basis voor de regressieanalyse, een statistische methode die sindsdien een onmisbaar instrument is geworden in diverse wetenschappelijke disciplines, van economie tot biologie.
Het belang van regressiecoëfficiënten kan niet worden overschat. Ze stellen ons in staat om data te interpreteren, voorspellingen te doen en weloverwogen beslissingen te nemen. Of het nu gaat om het optimaliseren van marketingcampagnes, het voorspellen van financiële trends of het bestuderen van de impact van klimaatverandering, regressiecoëfficiënten spelen een cruciale rol.
Een eenvoudig voorbeeld: stel dat een regressieanalyse aantoont dat een toename van €1000 in reclame-uitgaven leidt tot een toename van 100 verkochte producten. De regressiecoëfficiënt is dan 0.1 (100/1000). Dit betekent dat elke euro aan reclame leidt tot de verkoop van 0.1 product.
Voor- en nadelen van regressiecoëfficiënten
| Voordelen | Nadelen |
|---|---|
| Kwantificeert relaties tussen variabelen | Gevoelig voor outliers |
| Maakt voorspellingen mogelijk | Vereist aannames over de data |
| Helpt bij besluitvorming | Kan misleidend zijn bij niet-lineaire relaties |
Veelgestelde vragen:
1. Wat is een regressiecoëfficiënt? Een getal dat de verandering in de afhankelijke variabele weergeeft voor elke eenheidsverandering in de onafhankelijke variabele.
2. Hoe interpreteer je een regressiecoëfficiënt? De waarde geeft de sterkte en richting van de relatie tussen de variabelen aan.
3. Wat is het verschil tussen een positieve en een negatieve regressiecoëfficiënt? Een positieve coëfficiënt duidt op een positieve relatie, een negatieve op een negatieve relatie.
4. Hoe bereken je een regressiecoëfficiënt? Dit kan met behulp van statistische software of formules.
5. Wat is het belang van regressiecoëfficiënten? Ze helpen bij het begrijpen en voorspellen van relaties tussen variabelen.
6. Wat zijn de beperkingen van regressieanalyse? De analyse is gebaseerd op aannames die niet altijd geldig zijn.
7. Hoe gebruik je regressiecoëfficiënten in de praktijk? Voor het analyseren van data, het maken van voorspellingen en het nemen van beslissingen.
8. Waar kan ik meer informatie vinden over regressieanalyse? In statistische handboeken en online bronnen.
Tips en trucs: Gebruik betrouwbare software, controleer de aannames van de regressieanalyse en interpreteer de resultaten zorgvuldig.
Kortom, regressiecoëfficiënten zijn onmisbare instrumenten in de wereld van data-analyse. Ze ontsluiten de verborgen relaties in data en stellen ons in staat om weloverwogen beslissingen te nemen. Door de betekenis en interpretatie van deze getallen te begrijpen, kunnen we de kracht van data benutten en waardevolle inzichten verkrijgen. Of je nu een data scientist, marketeer, of gewoon nieuwsgierig bent naar de wereld om je heen, kennis van regressiecoëfficiënten is een waardevolle asset. De reis door de datawereld begint met het begrijpen van deze krachtige getallen. Dus duik in de data, ontdek de geheimen en ontgrendel de potentie van regressiecoëfficiënten. Verdiep je in de materie en ontdek hoe je deze tool kunt gebruiken om waardevolle inzichten te verkrijgen en de wereld om je heen beter te begrijpen. De mogelijkheden zijn eindeloos.

What Is Regression Coefficient Definition And Meaning | Kennecott Land

Introduction to Multiple Linear Regression | Kennecott Land
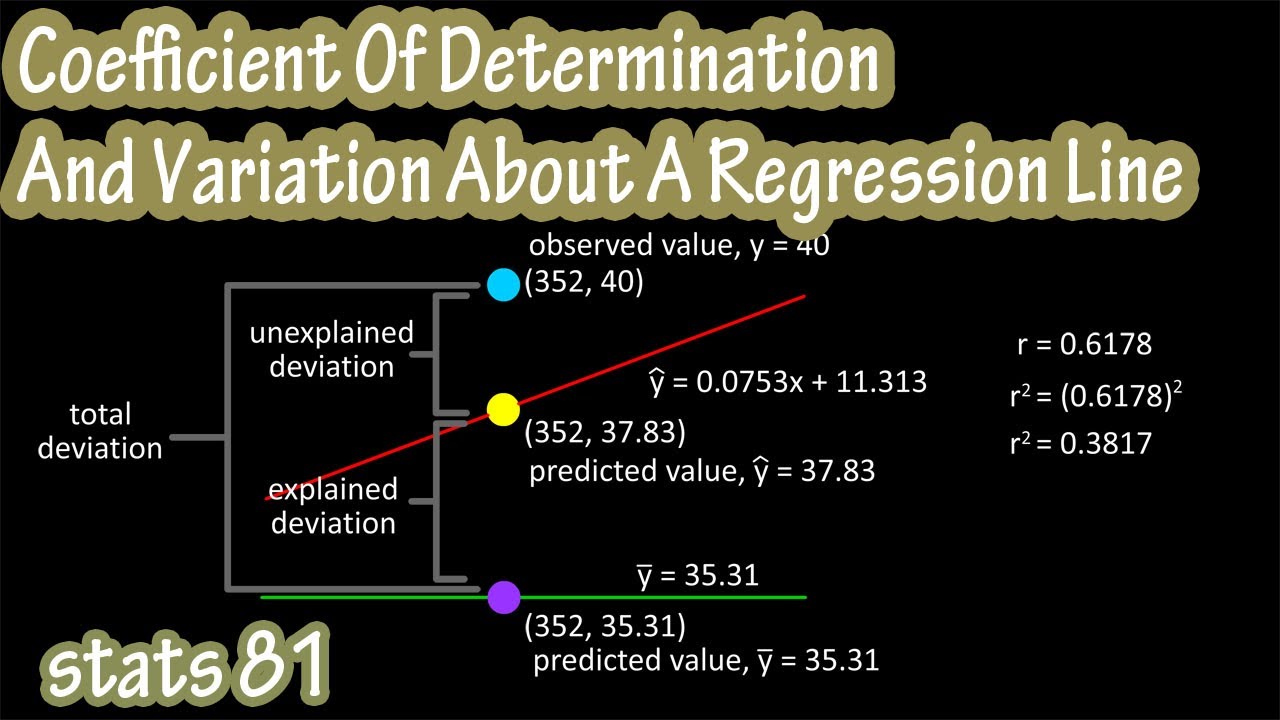
Tutustu 75 imagen coefficient of variation r studio | Kennecott Land

Understanding Linear Regression A Fundamental Tool for Predictive | Kennecott Land

How To Quickly Read the Output of Regression in Excel | Kennecott Land

what is a regression coefficient | Kennecott Land

Use Regression Coefficient In A Sentence | Kennecott Land

What is Regression Coefficient definition and meaning | Kennecott Land

How to Interpret Negative Coefficient Estimations in Linear Regression | Kennecott Land

Interpreting the Slope Intercept of a Linear Model | Kennecott Land

How to Calculate the Regression Coefficient of 4 Independent Variables | Kennecott Land

Equation of a linear regression model calculator | Kennecott Land

Linear Regression Equation Explained | Kennecott Land
:max_bytes(150000):strip_icc()/regression-4190330-ab4b9c8673074b01985883d2aae8b9b3.jpg)
Regression Definition Analysis Calculation and Example | Kennecott Land

Logistic regression in r | Kennecott Land