De Wondere Wereld van Zeshoeken in de Wiskunde
Stel je voor: een honingraat, de structuur van een voetbal, of zelfs de tegels op een oude straat. Wat hebben deze ogenschijnlijk willekeurige objecten gemeen? Ze zijn allemaal opgebouwd uit zeshoeken - een vorm die zowel in de natuur als in door de mens gemaakte constructies terug te vinden is. Maar wat maakt de zeshoek zo bijzonder, vooral in de wiskunde? Laten we dieper duiken in de fascinerende wereld van zeshoeken en hun unieke eigenschappen.
Een zeshoek, in de wiskunde, is een veelhoek met zes zijden en zes hoeken. Het is een veel voorkomende vorm in de geometrie en heeft een aantal interessante eigenschappen die hem nuttig maken in verschillende toepassingen. Vanwege zijn symmetrie en efficiënte pakking is de zeshoek een favoriet in zowel de natuur als de techniek.
De geschiedenis van zeshoeken gaat terug tot de oudheid. De Babyloniërs en Egyptenaren gebruikten ze al in hun architectuur en kunst. De Griekse wiskundige Pythagoras bestudeerde zeshoeken uitvoerig en ontdekte vele van hun unieke eigenschappen. Sindsdien hebben wiskundigen de zeshoek blijven bestuderen en zijn er talloze toepassingen voor gevonden in verschillende vakgebieden.
Een van de belangrijkste eigenschappen van een zeshoek is dat hij regelmatig kan zijn, wat betekent dat alle zijden even lang zijn en alle hoeken gelijk zijn. Een regelmatige zeshoek heeft zes gelijke zijden en zes gelijke hoeken van 120 graden. Deze symmetrie maakt de zeshoek tot een sterke en stabiele vorm, wat verklaart waarom hij zo vaak voorkomt in de natuur, zoals in de honingraten van bijen.
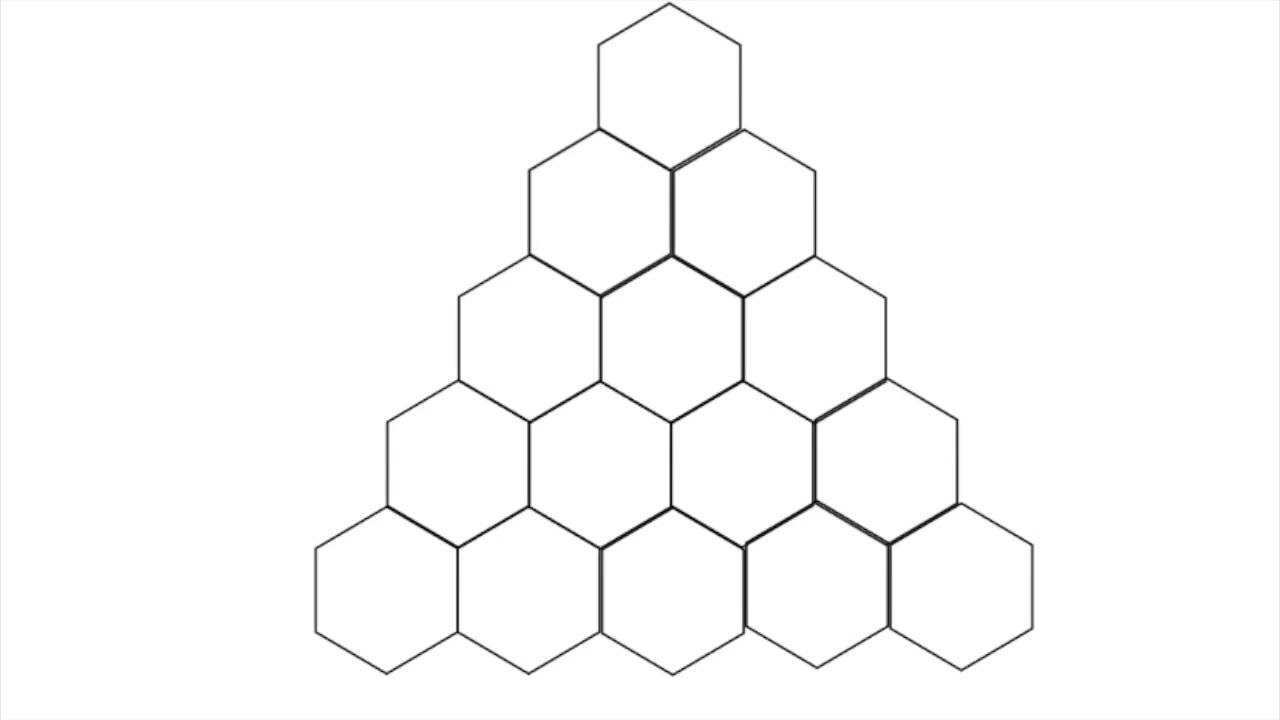
Naast zijn structurele eigenschappen, speelt de zeshoek ook een belangrijke rol in de wiskundige theorie. Het is een van de weinige regelmatige polygonen die een vlak volledig kunnen betegelen, wat betekent dat ze zonder gaten of overlappingen naast elkaar kunnen worden geplaatst. Deze eigenschap maakt zeshoeken nuttig in gebieden als tessellaties, verpakkingsproblemen en computergraphics.
Het begrijpen van de eigenschappen van zeshoeken is essentieel in verschillende toepassingen, van het ontwerpen van efficiënte structuren tot het ontwikkelen van geavanceerde wiskundige modellen. Of je nu een student bent die de basisprincipes van geometrie leert, een ingenieur die een nieuwe brug ontwerpt, of gewoon nieuwsgierig bent naar de wereld om je heen, de zeshoek is een fascinerende vorm met veel te bieden.
Voor- en Nadelen van Zeshoeken
| Voordelen | Nadelen |
|---|---|
| Efficiënte pakking | Beperkte ontwerpmogelijkheden |
| Structurele stabiliteit | Moeilijker te construeren dan vierkanten |
| Esthetisch aantrekkelijk | Niet zo veelzijdig als driehoeken |
Zeshoeken zijn alomtegenwoordig in ons dagelijks leven en in de wetenschap. Van honingraten tot de tegels op je vloer, hun unieke eigenschappen maken ze tot een fascinerend onderwerp van studie. Hopelijk heeft dit artikel je een beter begrip gegeven van wat een zeshoek is in de wiskunde en waarom deze vorm zo bijzonder is.

what is hexagon in maths | Kennecott Land

what is hexagon in maths | Kennecott Land

what is hexagon in maths | Kennecott Land

Using A Vector Method Find Op As A Simplified Expression In Terms Of A | Kennecott Land

what is hexagon in maths | Kennecott Land

what is hexagon in maths | Kennecott Land

what is hexagon in maths | Kennecott Land

what is hexagon in maths | Kennecott Land

Tetris Mosaic Animal Shape Childrens Puzzle Creative Fun Childrens | Kennecott Land

what is hexagon in maths | Kennecott Land

what is hexagon in maths | Kennecott Land

Question Video: Expressing Vectors in terms of 푢 and 푣 | Kennecott Land
what is hexagon in maths | Kennecott Land

Pythagoras Word Problems (With Clues) in 2024 | Kennecott Land

what is hexagon in maths | Kennecott Land