Dwarskracht en Buigmoment Formules: De Ultieme Gids
Ooit afgevraagd hoe bruggen en gebouwen zo sterk kunnen zijn? Het geheim zit hem in het begrijpen van dwarskracht en buigmoment. Deze krachten spelen een cruciale rol in de structurele analyse en het ontwerp van allerlei constructies. Het beheersen van de formules voor dwarskracht en buigmoment is essentieel voor ingenieurs en iedereen die betrokken is bij constructie.
Dwarskracht en buigmoment formules beschrijven hoe krachten zich gedragen binnen een structuur. Deze formules, vaak beschikbaar als handige PDF downloads, helpen ingenieurs de sterkte en stabiliteit van een constructie te berekenen. Zonder deze kennis zouden constructies instorten onder hun eigen gewicht of externe belastingen.
Het vinden van de juiste "shear force and bending moment formula pdf" kan een uitdaging zijn, maar deze gids helpt je op weg. We behandelen alles van de basisprincipes tot geavanceerde concepten, zodat je een volledig begrip krijgt van deze essentiële formules.
De formules voor dwarskracht en buigmoment zijn afgeleid van de basisprincipes van de statica. Ze stellen ons in staat om de interne krachten in een balk of andere structurele elementen te bepalen. Deze kennis is cruciaal voor het ontwerpen van veilige en efficiënte constructies.
In deze uitgebreide gids duiken we dieper in de wereld van dwarskracht en buigmoment. We bekijken de geschiedenis van deze formules, bespreken hun belang in de moderne engineering en bieden praktische voorbeelden om je te helpen de concepten te begrijpen.
De geschiedenis van deze formules gaat terug tot de ontwikkeling van de mechanica in de 17e en 18e eeuw. Wetenschappers zoals Galileo Galilei en Isaac Newton legden de basis voor het begrijpen van krachten en hun effect op structuren. Later werden deze principes verder ontwikkeld en toegepast op specifieke problemen in de bouwkunde.
Dwarskracht is de interne kracht die werkt loodrecht op de lengteas van een structureel element. Buigmoment is de interne kracht die probeert het element te buigen. Beide krachten zijn essentieel om te begrijpen hoe een structuur reageert op belastingen.
Voordelen van het gebruik van dwarskracht en buigmoment formules zijn: 1) Veiliger ontwerp: Door de krachten te berekenen, kunnen ingenieurs ervoor zorgen dat de structuur bestand is tegen de belastingen. 2) Efficiënt materiaalgebruik: Door de optimale afmetingen te bepalen, kan materiaalverspilling worden geminimaliseerd. 3) Betere prestatie: Door de vervormingen te berekenen, kan de prestatie van de structuur worden geoptimaliseerd.
Een checklist voor het toepassen van de formules: 1) Bepaal de belastingen op de structuur. 2) Teken een vrijlichaamsdiagram. 3) Pas de evenwichtsvergelijkingen toe. 4) Bereken de dwarskracht en het buigmoment op verschillende punten.
Voor- en Nadelen van het Gebruik van Dwarskracht en Buigmoment Formules
Hoewel het gebruik van dwarskracht en buigmoment formules essentieel is, zijn er ook enkele uitdagingen. Het kan complex zijn om de formules correct toe te passen, vooral bij complexe structuren. Daarom is het belangrijk om de juiste tools en software te gebruiken en de resultaten te controleren.
Veelgestelde vragen: 1) Wat is het verschil tussen dwarskracht en buigmoment? 2) Hoe bereken ik de dwarskracht en het buigmoment? 3) Waar kan ik een "shear force and bending moment formula pdf" vinden? 4) Wat zijn de belangrijkste toepassingen van deze formules? 5) Hoe kan ik de formules toepassen op complexe structuren? 6) Welke software kan ik gebruiken voor de berekeningen? 7) Wat zijn de meest voorkomende fouten bij het toepassen van de formules? 8) Hoe kan ik mijn berekeningen controleren?
Tips en trucs: Gebruik altijd de juiste eenheden. Controleer je berekeningen zorgvuldig. Maak gebruik van beschikbare software en online bronnen.
Kortom, het begrijpen en toepassen van dwarskracht en buigmoment formules is cruciaal voor het ontwerpen van veilige en efficiënte constructies. Door de principes van de mechanica te gebruiken en de juiste formules toe te passen, kunnen ingenieurs ervoor zorgen dat structuren bestand zijn tegen de belastingen waaraan ze worden blootgesteld. Het beheersen van deze concepten is essentieel voor iedereen die betrokken is bij de bouwsector. Blijf leren en ontwikkelen om je kennis van dwarskracht en buigmoment formules te verbeteren en bij te dragen aan de creatie van duurzame en veilige constructies voor de toekomst. Verder onderzoek en het raadplegen van experts is altijd aan te raden om de complexiteit van specifieke projecten aan te pakken en optimale resultaten te behalen. De juiste toepassing van deze principes draagt bij aan een veiligere en efficiëntere gebouwde omgeving voor iedereen.

Understanding the Bending Moment Diagram of a Beam A Comprehensive Guide | Kennecott Land

Bending Moment And Shear Force Formulas | Kennecott Land
Simply Supported UDL Beam Formulas | Kennecott Land

Shear And Moment Diagrams For Beams | Kennecott Land

Learn how to draw shear force and bending moment diagrams | Kennecott Land

Learn How To Draw Shear Force And Bending Moment Diagrams | Kennecott Land

Shear Force Bending Moment Diagram For Civil And Engineering | Kennecott Land

Brief Information About Shear Force And Bending Moment Diagrams | Kennecott Land

Portal Frame Worked Example | Kennecott Land

Brief Information About Shear Force And Bending Moment Diagrams | Kennecott Land

Bending Moment Diagram Of Continuous Beam | Kennecott Land

Pin on Construction World | Kennecott Land
Simply Supported UDL Beam Formulas | Kennecott Land
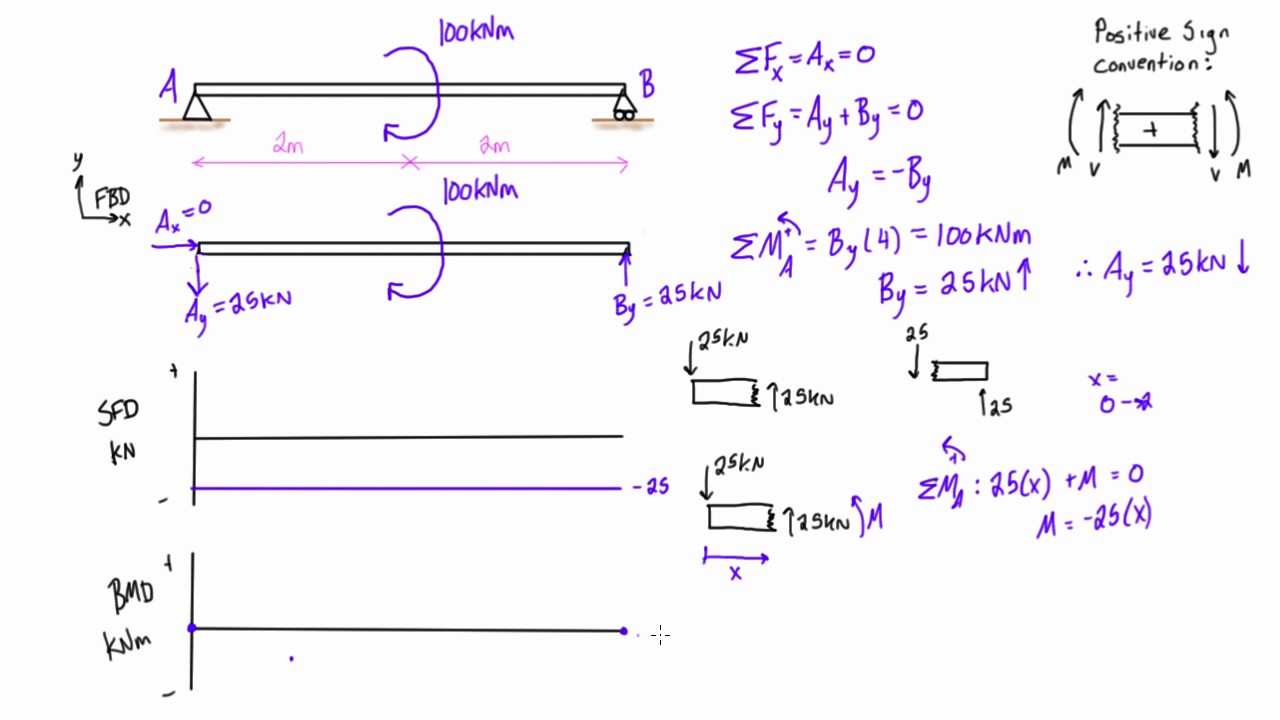
DIAGRAM Shear Force And Bending Moment Diagram Solved Examples | Kennecott Land

Bending Moment Diagram Table | Kennecott Land