Hoeken Berekenen in Rechthoekige Driehoeken Ontrafeld

12 Aug 2024

Hoe Bereken Je Een Hoek Van Een Driehoek Een Eenvoudige Uitleg

Stel je voor: je staat voor een steile berg en wilt de hoek berekenen die de helling maakt met de grond. Of je bent een architect die de perfecte hoek voor een dak ontwerpt. In beide gevallen heb je kennis nodig van het berekenen van hoeken in rechthoekige driehoeken. Deze ogenschijnlijk eenvoudige geometrische figuur speelt een cruciale rol in talloze toepassingen, van navigatie tot constructie.

Het bepalen van hoeken in rechthoekige driehoeken is een fundamenteel concept in de trigonometrie. Deze tak van de wiskunde bestudeert de relaties tussen hoeken en zijden van driehoeken. Specifiek voor rechthoekige driehoeken, waar één hoek altijd 90 graden is, gebruiken we trigonometrische functies zoals sinus, cosinus en tangens.

De oorsprong van trigonometrie gaat terug tot de oude Grieken en Egyptenaren die deze principes gebruikten voor landmeting en astronomie. Hun kennis legde de basis voor de moderne trigonometrie die we vandaag de dag kennen.

Het belang van het kunnen berekenen van hoeken in rechthoekige driehoeken strekt zich uit tot vele disciplines. In de natuurkunde, bijvoorbeeld, worden deze berekeningen gebruikt om de baan van projectielen te bepalen. In de bouwkunde zijn ze essentieel voor het ontwerpen van stabiele structuren. Zelfs in de computergraphics spelen ze een rol bij het renderen van 3D-beelden.

Een veelvoorkomend probleem bij het berekenen van hoeken is het correct toepassen van de trigonometrische functies. Het is belangrijk om de juiste functie te kiezen op basis van de gegeven zijden. Verwarring tussen sinus, cosinus en tangens kan leiden tot onnauwkeurige resultaten.

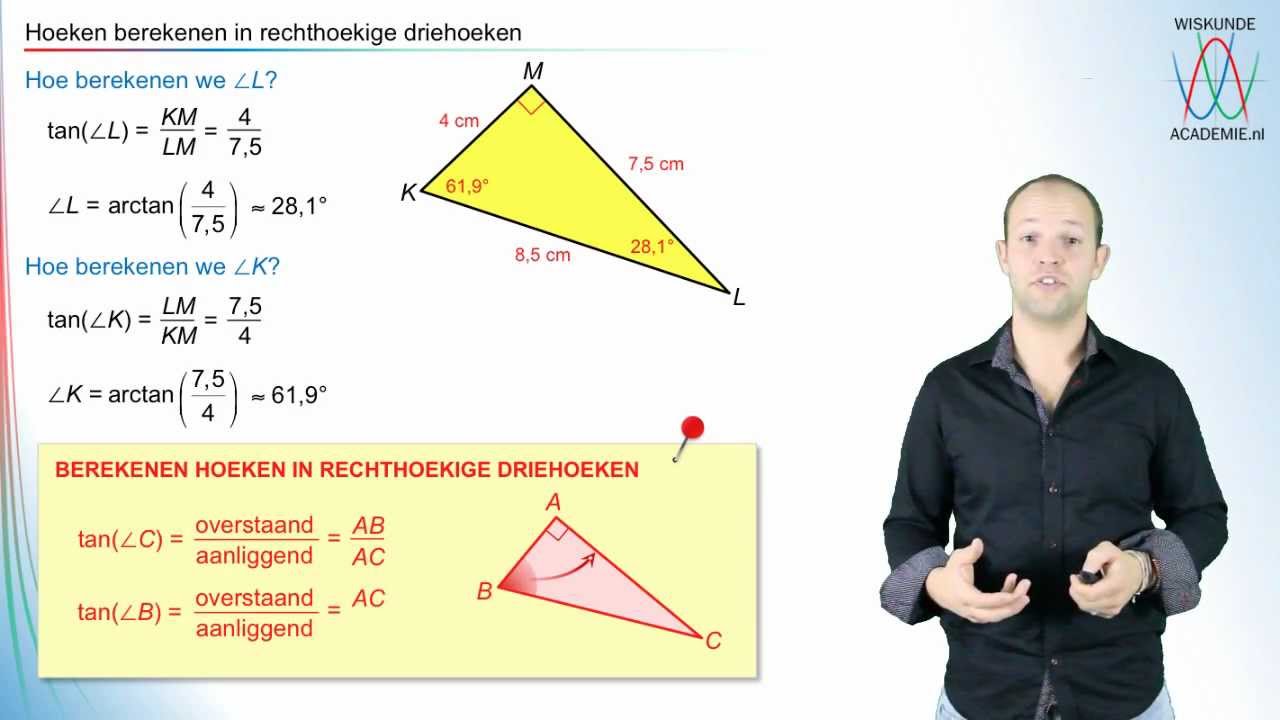
Om de hoeken te bepalen, gebruiken we de trigonometrische functies. Sinus (sin) is de verhouding tussen de overstaande zijde en de schuine zijde. Cosinus (cos) is de verhouding tussen de aanliggende zijde en de schuine zijde. Tangens (tan) is de verhouding tussen de overstaande zijde en de aanliggende zijde.

Voorbeeld: In een rechthoekige driehoek met een overstaande zijde van 3 cm en een aanliggende zijde van 4 cm, is de tangens van de hoek gelijk aan 3/4 = 0.75. De hoek zelf kan worden berekend met de inverse tangens (arctan) functie: arctan(0.75) ≈ 36.87 graden.

Voordelen van het beheersen van deze vaardigheid zijn onder andere: nauwkeurige metingen in diverse vakgebieden, beter begrip van geometrische principes en verbeterde probleemoplossende vaardigheden.

Een actieplan voor het berekenen van hoeken omvat: identificeren van de bekende zijden, kiezen van de juiste trigonometrische functie en het gebruiken van een rekenmachine om de hoek te berekenen.

Checklist: Ken je de overstaande en aanliggende zijde? Heb je de juiste functie (sin, cos, tan) gekozen? Heb je de inverse functie gebruikt om de hoek te vinden?

Stap-voor-stap handleiding: 1. Identificeer de rechthoekige driehoek. 2. Bepaal welke zijden bekend zijn. 3. Kies de juiste trigonometrische functie. 4. Bereken de verhouding. 5. Gebruik de inverse functie om de hoek te vinden.

Voor- en Nadelen

Voordelen	Nadelen
Essentieel voor diverse vakgebieden	Vereist begrip van trigonometrische functies

Beste praktijken: Teken altijd een diagram, label de zijden correct, controleer je berekeningen, gebruik een rekenmachine met graden-instelling, en oefen regelmatig.

Voorbeelden: Berekenen van de hellingshoek van een dak, bepalen van de hoogte van een boom met behulp van schaduw, berekenen van de hoek van een projectiel, navigatie met behulp van kompas en kaart, ontwerpen van bruggen en gebouwen.

Uitdagingen: Onnauwkeurige metingen, verkeerde keuze van trigonometrische functie. Oplossingen: Dubbelcheck metingen, zorgvuldig kiezen van de juiste functie.

FAQ: Wat is sinus? Wat is cosinus? Wat is tangens? Hoe gebruik ik de inverse functies? Wat is een rechthoekige driehoek? Hoe identificeer ik de overstaande en aanliggende zijde? Wanneer gebruik ik sinus, cosinus of tangens? Waar kan ik meer informatie vinden?

Tips: Oefen met verschillende soorten driehoeken. Gebruik online tools en apps om je begrip te verdiepen. Maak gebruik van ezelsbruggetjes om de functies te onthouden.

Het berekenen van hoeken in rechthoekige driehoeken is een essentiële vaardigheid met brede toepasbaarheid in diverse disciplines. Van het ontwerpen van gebouwen tot het navigeren door de wereld om ons heen, begrip van trigonometrische principes stelt ons in staat om complexe problemen op te lossen en nauwkeurige metingen uit te voeren. Door de hierboven beschreven stappen, tips en voorbeelden te volgen, kan iedereen deze waardevolle vaardigheid beheersen. Blijf oefenen en ontdek de kracht van trigonometrie in je dagelijks leven. Het beheersen van deze vaardigheid opent deuren naar een dieper begrip van de wereld om ons heen, van de architectuur van gebouwen tot de banen van planeten. De mogelijkheden zijn eindeloos, en de kennis die je opdoet zal je gedurende je hele leven van dienst zijn. Dus pak je rekenmachine, teken een driehoek en begin met verkennen!