Ontdek de geheimen van de lange zijde: Berekeningen en meer!
Hoe vind je de lengte van die mysterieuze lange zijde, de hypotenusa van een rechthoekige driehoek? Deze vraag houdt velen bezig, van studenten die worstelen met wiskunde tot architecten die complexe constructies ontwerpen. Het bepalen van de lengte van de lange zijde is een fundamenteel concept in de geometrie en heeft talloze toepassingen in de praktijk.
De sleutel tot het ontsluiten van dit mysterie ligt in de stelling van Pythagoras. Deze eeuwenoude stelling legt een elegante relatie vast tussen de zijden van een rechthoekige driehoek. Maar wat als je geen rechthoekige driehoek hebt? Dan zijn er andere methoden, zoals de cosinusregel, die je kunnen helpen.
Het berekenen van de lange zijde is meer dan alleen een wiskundige oefening. Het is een essentiële vaardigheid die ons helpt de wereld om ons heen te begrijpen en te manipuleren. Van het bepalen van de afstand tussen twee punten tot het ontwerpen van stabiele constructies, de toepassingen zijn eindeloos.
De stelling van Pythagoras, genoemd naar de Griekse filosoof Pythagoras, stelt dat in een rechthoekige driehoek het kwadraat van de lengte van de hypotenusa (de lange zijde) gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden (de rechthoekszijden). Dit kan worden weergegeven met de formule a² + b² = c², waarbij c de lengte van de hypotenusa is en a en b de lengtes van de rechthoekszijden.
De oorsprong van de stelling van Pythagoras gaat terug tot de Babyloniërs en Egyptenaren, lang vóór Pythagoras zelf. Echter, Pythagoras en zijn volgelingen worden gecrediteerd voor het formele bewijs van de stelling. Het belang van deze stelling kan niet worden overschat. Het vormt de basis van vele andere wiskundige concepten en heeft een enorme impact gehad op de ontwikkeling van de wiskunde en wetenschap.
Voorbeeld: Stel je een rechthoekige driehoek voor met rechthoekszijden van 3 en 4 cm. Om de lengte van de hypotenusa te berekenen, gebruiken we de stelling van Pythagoras: 3² + 4² = c². Dus, 9 + 16 = c², 25 = c², en c = 5 cm.
Voordelen van het kunnen berekenen van de lange zijde:
1. Ontwerpen en constructie: Essentieel voor architecten, ingenieurs en bouwers.
2. Navigatie: Het bepalen van afstanden en routes.
3. Computergraphics en gaming: Creëren van realistische 3D-modellen.
Stap-voor-stap handleiding:
1. Identificeer de rechthoekige driehoek.
2. Bepaal de lengtes van de rechthoekszijden (a en b).
3. Pas de stelling van Pythagoras toe: a² + b² = c².
4. Bereken c door de wortel van c² te nemen.
Voor- en Nadelen van de Stelling van Pythagoras
Er zijn geen echte nadelen aan de stelling zelf, maar wel aan de toepasbaarheid ervan. Het is alleen direct toepasbaar op rechthoekige driehoeken.
Veelgestelde vragen:
1. Wat is de stelling van Pythagoras? Antwoord: a² + b² = c²
2. Wat is de hypotenusa? Antwoord: De lange zijde van een rechthoekige driehoek.
3. Kan ik de stelling van Pythagoras gebruiken voor andere driehoeken? Antwoord: Nee, alleen voor rechthoekige driehoeken.
4. Wat als ik de lengte van één rechthoekszijde en de hypotenusa ken? Antwoord: Je kunt de stelling herschrijven om de onbekende zijde te vinden.
5. Waar kan ik meer informatie vinden over de stelling van Pythagoras? Antwoord: Online bronnen en wiskundeboeken.
6. Hoe bereken ik de diagonaal van een rechthoek? Antwoord: Met de stelling van Pythagoras, want de diagonaal vormt de hypotenusa van een rechthoekige driehoek.
7. Wat is een praktische toepassing van de stelling van Pythagoras? Antwoord: Het berekenen van de afstand tussen twee punten op een kaart.
8. Hoe kan ik de stelling van Pythagoras visualiseren? Antwoord: Door een tekening te maken van een rechthoekige driehoek en de kwadraten op elke zijde te tekenen.
Tips en trucs: Zorg ervoor dat je de juiste eenheden gebruikt en rond je antwoord af op het juiste aantal significante cijfers.
Conclusie: Het berekenen van de lange zijde, of hypotenusa, van een rechthoekige driehoek met behulp van de stelling van Pythagoras is een fundamentele vaardigheid met brede toepassingen in verschillende disciplines. Van architectuur tot navigatie, het begrijpen en toepassen van dit concept is essentieel. Het beheersen van deze vaardigheid opent deuren naar een dieper begrip van de wereld om ons heen en stelt ons in staat om problemen op te lossen met precisie en efficiëntie. Dus, neem de tijd om de stelling van Pythagoras te oefenen en te begrijpen, het zal je zeker van pas komen! Door de geschiedenis en de praktische toepassingen te begrijpen, wordt wiskunde niet alleen een abstract concept, maar een krachtig hulpmiddel om de wereld te begrijpen. Blijf oefenen met verschillende voorbeelden en ontdek de kracht van de stelling van Pythagoras!

Hoe Bereken Je De Vierkante Meter | Kennecott Land

Hoe Bereken Ik Vierkante Meters | Kennecott Land

Hoe bereken je een driehoek | Kennecott Land
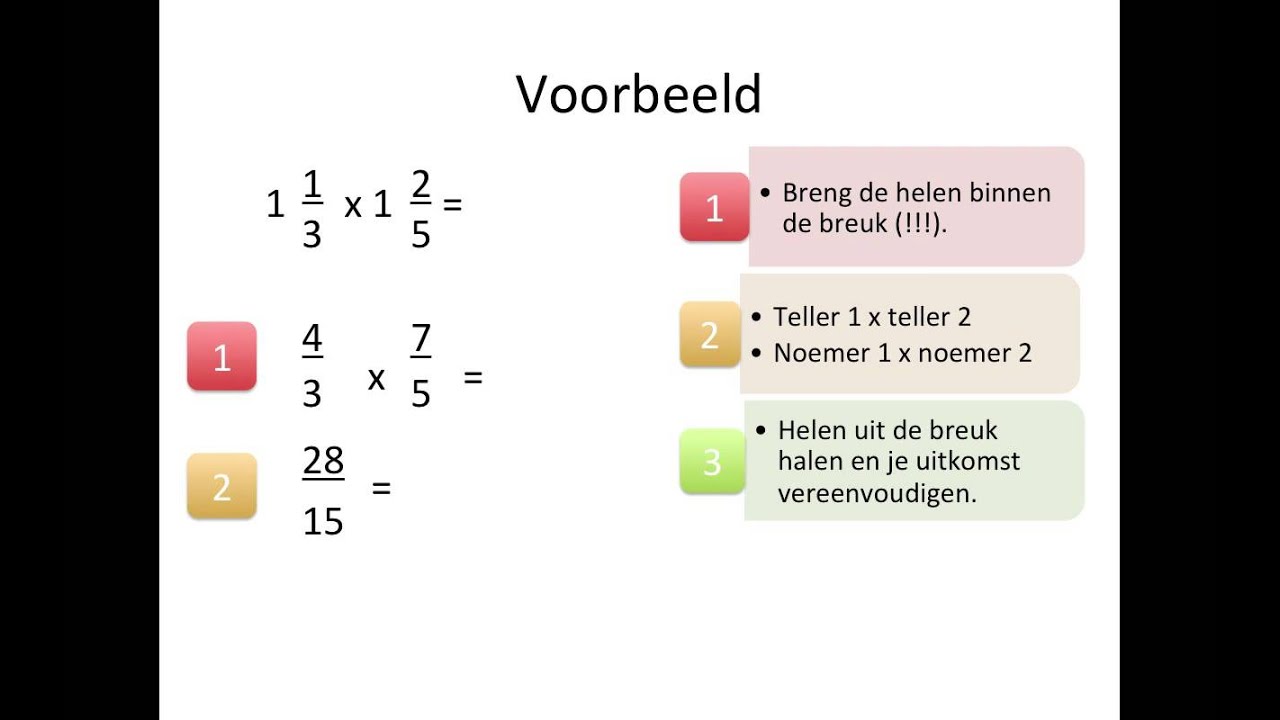
Hoe Bereken Je Het Gemiddeld Eigen Vermogen | Kennecott Land
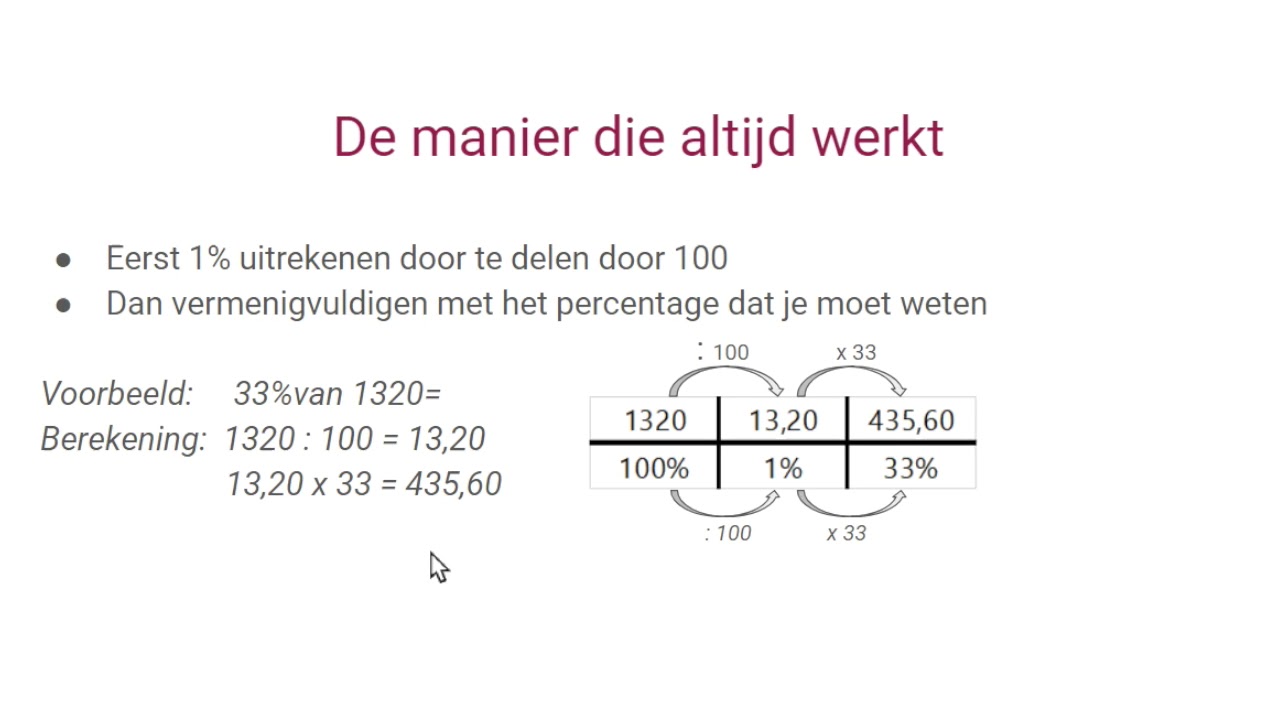
Hoe Bereken Je Gemiddeld Uit | Kennecott Land
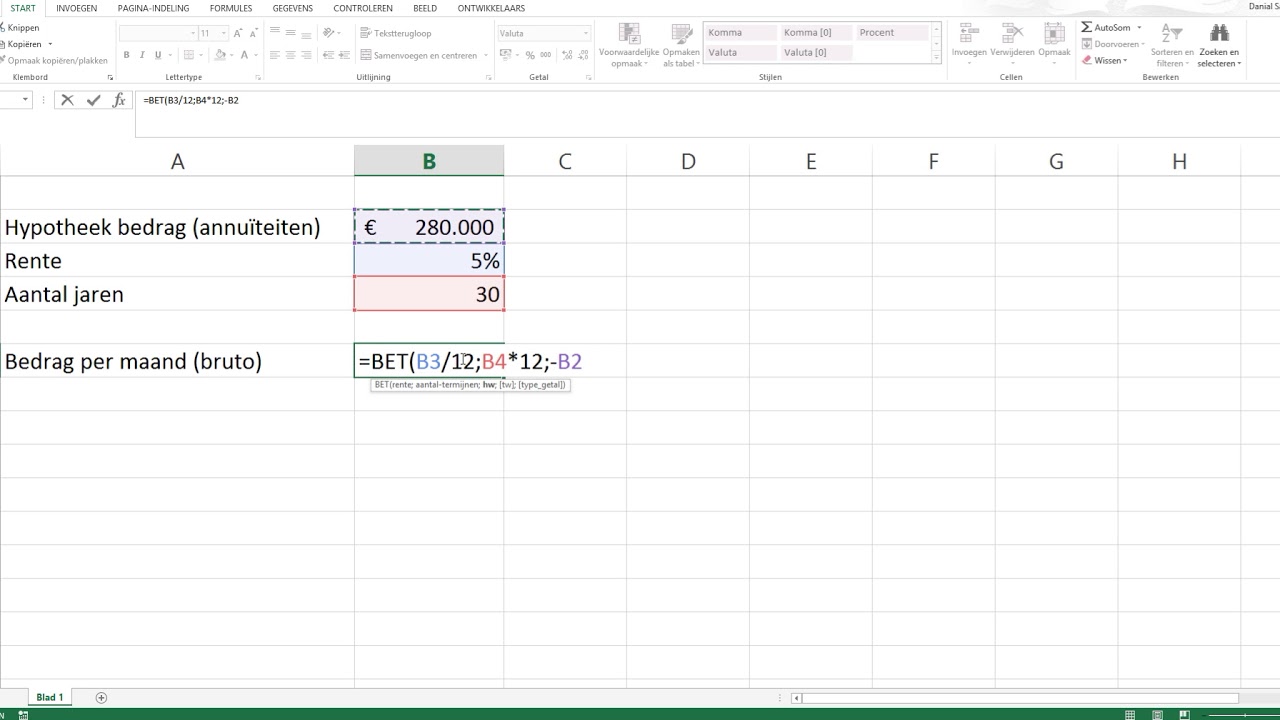
Hoe Bereken Je Wettelijke Rente | Kennecott Land
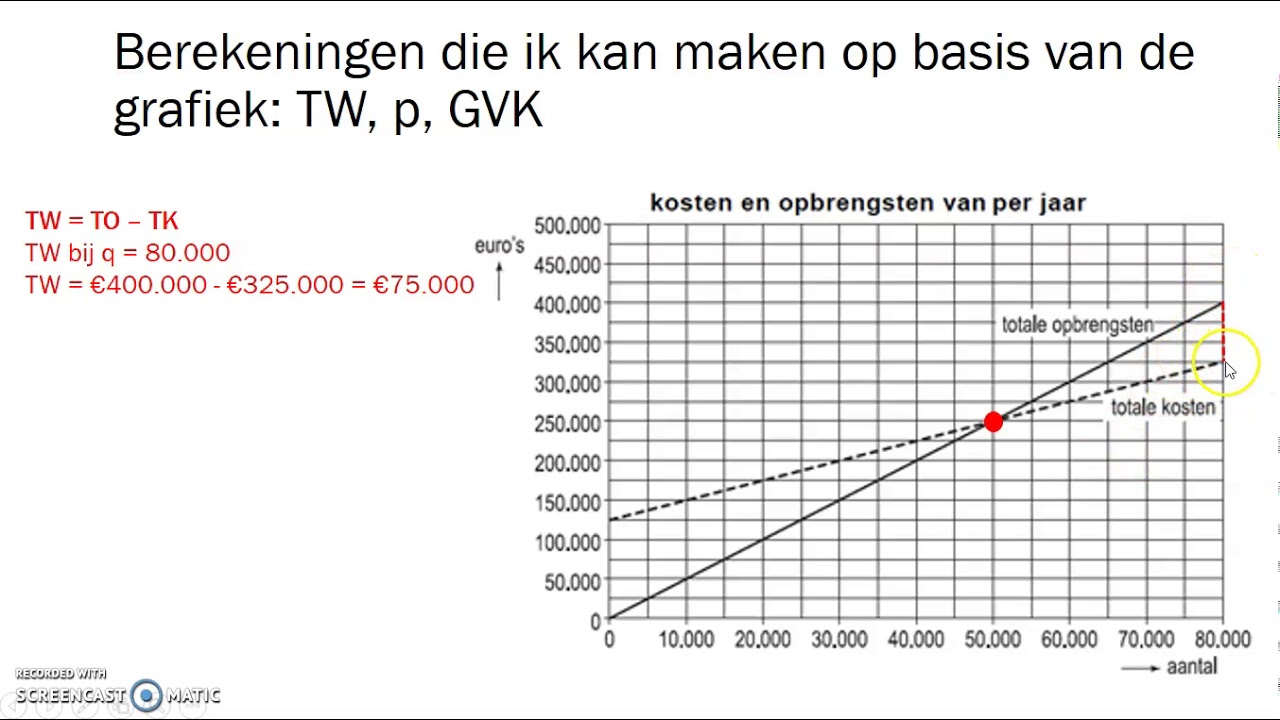
Wat Zijn Variabele Kosten | Kennecott Land

Hoe Bereken Je De Variabele Kosten | Kennecott Land

Hoe bereken je de terugverdientijd van zonnepanelen | Kennecott Land
Hoe Bereken Je Vierkante Meter | Kennecott Land

Hoe Bereken Je Het Gemiddeld Eigen Vermogen | Kennecott Land

hoe bereken je de lange zijde | Kennecott Land

Hoe Bereken Je De Brutowinstmarge Een Eenvoudige Gids | Kennecott Land

Hoe Bereken Je Vierkante Meter | Kennecott Land

Hoe bereken je de terugverdientijd van zonnepanelen | Kennecott Land