Ontdek de Wereld van Tangens: Een Praktische Gids

23 Sep 2024

Stel je voor: je staat voor een enorme piramide, de zon brandt op je gezicht. Je wilt de hoogte weten, maar hoe? Of je ontwerpt een dak voor je droomhuis en je moet de perfecte hoek berekenen. Dit zijn slechts twee voorbeelden waar de tangens, een krachtig wiskundig concept, van pas komt. Maar wat is de tangens nu precies en hoe kan het ons helpen de wereld om ons heen te begrijpen?

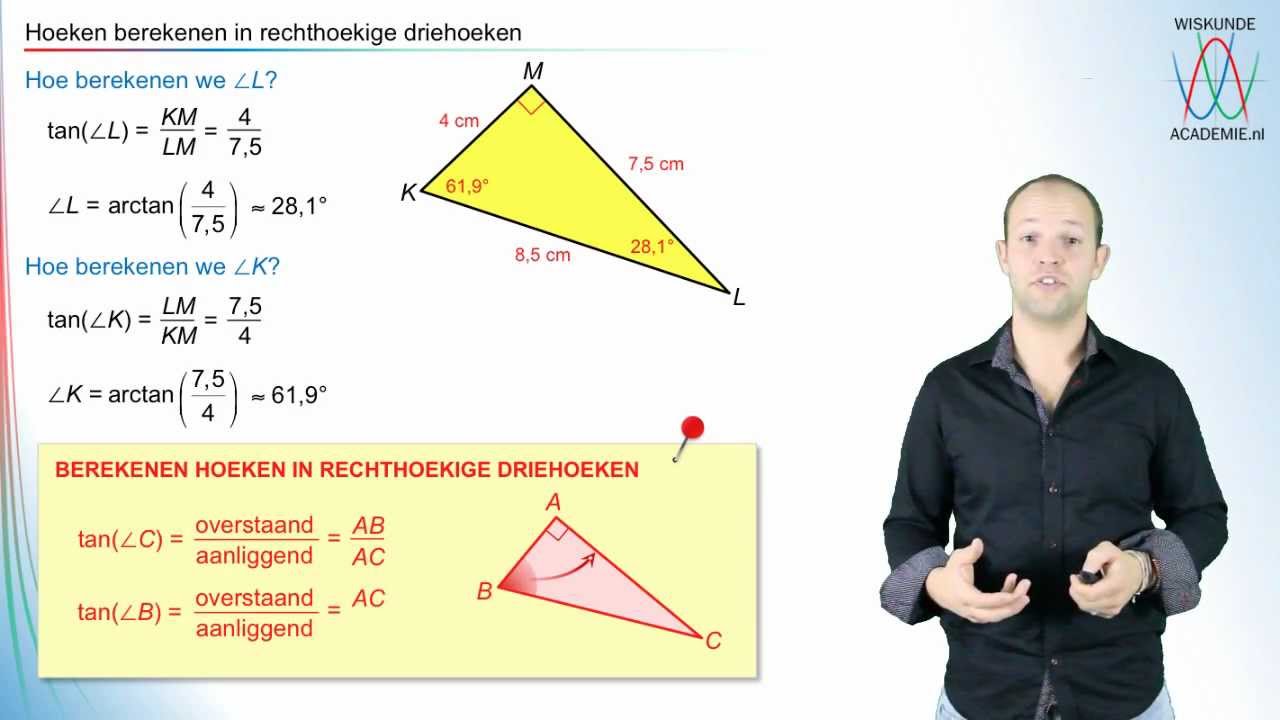
Simpel gezegd, de tangens is een trigonometrische functie die de verhouding beschrijft tussen de overstaande en de aanliggende zijde van een rechthoekige driehoek. Het is als een magische code die ons in staat stelt om onbekende lengtes en hoeken te ontrafelen met behulp van de kracht van wiskunde. Van het meten van de hoogte van bergen tot het navigeren over oceanen, de tangens heeft een lange en rijke geschiedenis vol fascinerende toepassingen.

Het begrip tangens is al eeuwenlang bekend. Oude beschavingen, zoals de Babyloniërs en Egyptenaren, gebruikten het om astronomische berekeningen te maken en piramides te bouwen. De Griekse astronoom Hipparchus wordt beschouwd als de vader van de trigonometrie, en zijn werk legde de basis voor ons moderne begrip van de tangens.

Tegenwoordig is de tangens niet alleen een essentieel hulpmiddel in de wiskunde, maar ook in verschillende andere vakgebieden, waaronder natuurkunde, techniek, architectuur en informatica. Het wordt gebruikt om alles te berekenen, van de baan van projectielen tot de intensiteit van lichtgolven.

Laten we eens kijken naar een eenvoudig voorbeeld om de kracht van de tangens te illustreren. Stel je een rechthoekige driehoek voor met een hoek van 30 graden. De overstaande zijde van deze hoek is 5 cm lang. We kunnen de tangens gebruiken om de lengte van de aanliggende zijde te berekenen. De tangens van 30 graden is ongeveer 0,58. Dus, we delen de lengte van de overstaande zijde (5 cm) door de tangens van 30 graden (0,58) en krijgen we ongeveer 8,6 cm. Dit is de lengte van de aanliggende zijde.

Voordelen en Nadelen van Tangens

Zoals met elk wiskundig concept zijn er voordelen en nadelen aan het gebruik van tangens. Laten we eens kijken:

Voordelen	Nadelen
Veelzijdig: Kan worden gebruikt in verschillende vakgebieden en toepassingen.	Kan complex zijn: Vereist een goed begrip van trigonometrie en rechthoekige driehoeken.
Krachtig: Maakt nauwkeurige berekeningen mogelijk van onbekende lengtes en hoeken.	Beperkt tot rechthoekige driehoeken: Kan niet worden gebruikt met andere soorten driehoeken.
Toegankelijk: Gemakkelijk te berekenen met behulp van rekenmachines en computerprogramma's.	Gevoelig voor fouten: Kleine meetfouten kunnen leiden tot grote onnauwkeurigheden in berekeningen.

Kortom, de tangens is een essentieel hulpmiddel voor iedereen die geïnteresseerd is in wiskunde, wetenschap, techniek of andere vakgebieden. Door de kracht van de tangens te begrijpen en te gebruiken, kunnen we de wereld om ons heen op nieuwe en opwindende manieren verkennen en begrijpen. Dus ga erop uit, ontdek de wereld van de tangens en zie wat je kunt creëren!