Ontdek de Wondere Wereld van Tangens: Van Driehoeken tot Trigonometrie
Heb je je ooit afgevraagd hoe je de hoogte van een boom kunt berekenen zonder hem te beklimmen? Of hoe zit het met het bepalen van de afstand tot een schip op zee? Het antwoord ligt in een fascinerend stukje wiskunde dat bekend staat als trigonometrie, en in het bijzonder in de functie 'tangens'. In deze blog duiken we in de wondere wereld van tangens en ontdekken we hoe deze ogenschijnlijk eenvoudige functie een wereld van mogelijkheden opent in de wiskunde, natuurkunde en ons dagelijks leven.
De term 'tangens' komt van het Latijnse woord 'tangere', wat 'aanraken' betekent. En dat is precies wat het doet! In een rechthoekige driehoek beschrijft de tangens van een hoek de verhouding tussen de lengte van de overstaande zijde en de lengte van de aanliggende zijde. Het is als een magische code die ons in staat stelt om onbekende afstanden en hoeken te ontrafelen, waardoor we de geheimen van de geometrie kunnen ontsluieren.
Maar tangens is veel meer dan alleen een wiskundige tool. Het heeft een lange en rijke geschiedenis die teruggaat tot de oude beschavingen, waar het werd gebruikt voor navigatie, landmeting en zelfs astronomie. Vandaag de dag vinden we toepassingen van tangens in uiteenlopende gebieden, van architectuur en engineering tot computergraphics en muziek.
Het mooie van tangens is dat het, ondanks zijn kracht en veelzijdigheid, verrassend eenvoudig te begrijpen en toe te passen is. Met een beetje oefening kan iedereen de basisprincipes van tangens onder de knie krijgen en de magie van trigonometrie in actie zien. Of je nu een student bent die worstelt met wiskunde, een professional die zijn vaardigheden wil opfrissen, of gewoon nieuwsgierig bent naar de wereld om je heen, deze blog neemt je mee op een spannende reis door de wonderlijke wereld van tangens.
Dus leun achterover, ontspan en maak je klaar om de geheimen van tangens te ontdekken! In de volgende paragrafen zullen we dieper ingaan op de geschiedenis, de toepassingen en de vele voordelen van deze fascinerende trigonometrische functie. Bereid je voor om versteld te staan van de kracht en elegantie van tangens en de manier waarop het onze kijk op de wereld om ons heen kan veranderen.
Voor- en nadelen van het gebruiken van tangens
Zoals met alle wiskundige concepten, zijn er voor- en nadelen aan het gebruiken van tangens:
| Voordelen | Nadelen |
|---|---|
| Nuttig voor het berekenen van hoeken en afstanden in rechthoekige driehoeken. | Alleen van toepassing op rechthoekige driehoeken. |
| Toepasbaar in verschillende vakgebieden zoals natuurkunde, engineering en architectuur. | Vereist nauwkeurige metingen voor nauwkeurige resultaten. |
| Relatief eenvoudig te begrijpen en toe te passen met basiskennis van trigonometrie. | Kan complex worden bij gebruik in geavanceerde trigonometrische problemen. |
Tips en trucs voor het werken met tangens
Hier zijn een paar handige tips en trucs om te onthouden bij het werken met tangens:
- Zorg ervoor dat je te maken hebt met een rechthoekige driehoek voordat je de tangensfunctie toepast.
- Onthoud de afkorting SOH CAH TOA om de trigonometrische verhoudingen te onthouden. TOA staat voor Tangens = Overstaande / Aanliggende.
- Gebruik een wetenschappelijke rekenmachine of trigonometrische tabellen om de tangens van een hoek te vinden.
- Oefen regelmatig met het oplossen van trigonometrische problemen met tangens om je vaardigheden te verbeteren.
Conclusie
Tangens is een krachtige en veelzijdige trigonometrische functie die een breed scala aan toepassingen heeft in verschillende vakgebieden. Van het berekenen van afstanden tot het oplossen van complexe technische problemen, tangens speelt een cruciale rol in ons begrip van de wereld om ons heen. Hoewel het enkele uitdagingen met zich mee kan brengen, maken de voordelen van het beheersen van tangens het de moeite waard om te leren. Dus ga je gang, duik in de wereld van trigonometrie en ontdek de vele wonderen van tangens!

Trigonometrie (Winkelfunktion) am Einheitskreis online erklärt | Kennecott Land

was ist ein tangens | Kennecott Land

was ist ein tangens | Kennecott Land

Gase in Endlagern im Salz | Kennecott Land

was ist ein tangens | Kennecott Land

was ist ein tangens | Kennecott Land

Johann adam kuchenreuter in regensburg | Kennecott Land

Trigonometrie Erklärung mit Formeln und Beispielen | Kennecott Land

Johann adam kuchenreuter in regensburg | Kennecott Land

was ist ein tangens | Kennecott Land

was ist ein tangens | Kennecott Land

Sinus Und Cosinus Tabelle | Kennecott Land

was ist ein tangens | Kennecott Land
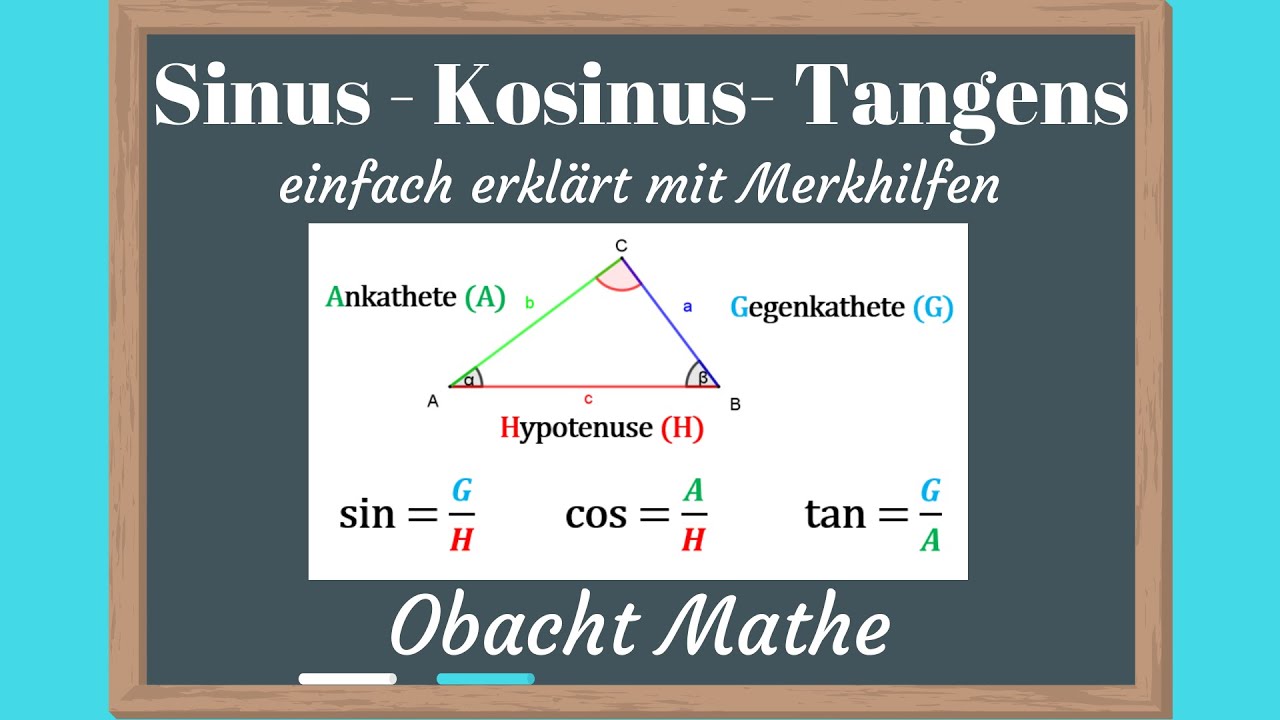
was ist ein tangens | Kennecott Land
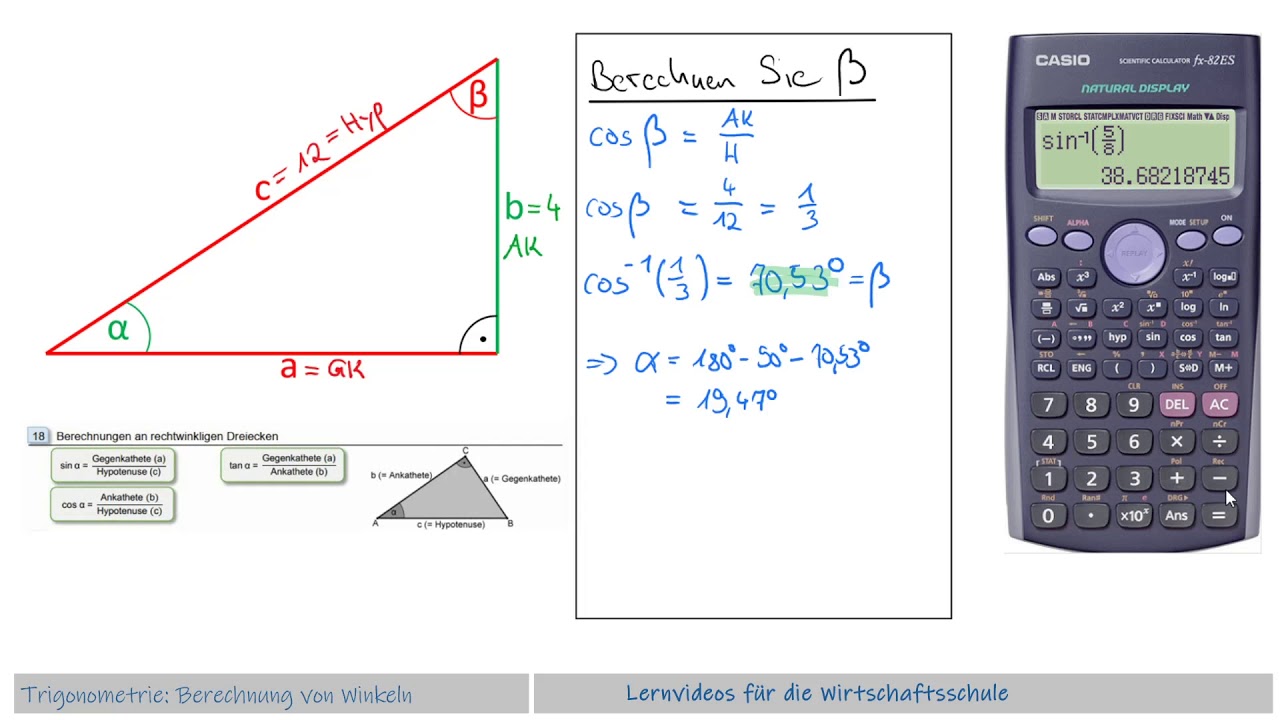
Formelsammlung Trigonometrie Formelsammlung Trigonometrie | Kennecott Land