Regressievergelijking vinden: De Ultieme Gids
Hoe vind je een regressievergelijking? Deze vraag speelt een cruciale rol in tal van disciplines, van economie tot biologie en van sociologie tot engineering. Het stelt ons in staat om relaties tussen variabelen te modelleren en voorspellingen te doen over de toekomst. Stel je voor dat je de impact van reclame-uitgaven op de verkoop wilt begrijpen. Een regressievergelijking kan je helpen deze relatie te kwantificeren en te voorspellen hoeveel de verkoop zal stijgen met een bepaalde toename in reclame-uitgaven.
Het bepalen van een regressievergelijking opent de deur naar een dieper begrip van de wereld om ons heen. Door data te analyseren en patronen te ontdekken, kunnen we inzichten verkrijgen die anders verborgen zouden blijven. Of het nu gaat om het voorspellen van de groei van een populatie, het optimaliseren van productieprocessen of het evalueren van de effectiviteit van een nieuw medicijn, regressieanalyse is een onmisbaar hulpmiddel.
De zoektocht naar de juiste regressievergelijking begint met het verzamelen van relevante data. Deze data vertegenwoordigen de variabelen die je wilt analyseren. Vervolgens gebruik je statistische methoden om een vergelijking te vinden die de relatie tussen deze variabelen het beste beschrijft. Er zijn verschillende soorten regressieanalyse, zoals lineaire regressie, meervoudige regressie en logistische regressie, elk geschikt voor verschillende soorten data en onderzoeksvragen.
Het concept van regressie werd geïntroduceerd door Sir Francis Galton in de 19e eeuw tijdens zijn onderzoek naar de relatie tussen de lengte van ouders en hun kinderen. Hij merkte op dat extreem lange ouders de neiging hadden om kinderen te krijgen die iets minder lang waren dan zijzelf, terwijl extreem korte ouders de neiging hadden om kinderen te krijgen die iets langer waren dan zijzelf. Dit fenomeen noemde hij "regressie naar het gemiddelde". Sindsdien heeft regressieanalyse zich ontwikkeld tot een krachtige statistische methode met brede toepassingen.
Een belangrijk probleem bij het vinden van een regressievergelijking is het kiezen van het juiste model. Een te simpel model kan de relatie tussen de variabelen niet accuraat weergeven, terwijl een te complex model kan leiden tot overfitting, waarbij het model te goed past bij de trainingsdata maar slecht presteert op nieuwe data. Het is daarom essentieel om de juiste balans te vinden tussen modelcomplexiteit en modelprestatie.
Een eenvoudige lineaire regressievergelijking heeft de vorm y = mx + b, waarbij y de afhankelijke variabele is, x de onafhankelijke variabele, m de helling en b het snijpunt met de y-as. De helling geeft aan hoeveel y verandert voor elke eenheidsverandering in x, terwijl het snijpunt de waarde van y aangeeft wanneer x gelijk is aan nul.
Voordelen van regressieanalyse zijn: 1) Voorspellingen maken: Door de regressievergelijking te gebruiken, kun je voorspellingen maken over de waarde van de afhankelijke variabele op basis van de waarde van de onafhankelijke variabele. 2) Relaties begrijpen: Regressieanalyse helpt bij het begrijpen van de aard en sterkte van de relatie tussen variabelen. 3) Controle voor confounders: Meervoudige regressie maakt het mogelijk om de invloed van meerdere onafhankelijke variabelen tegelijk te analyseren, waardoor je kunt controleren voor confounders.
Voor- en Nadelen van Regressieanalyse
| Voordelen | Nadelen |
|---|---|
| Voorspellingen maken | Gevoelig voor outliers |
| Relaties begrijpen | Vereist aannames over de data |
| Controle voor confounders | Kan misleidend zijn bij niet-lineaire relaties |
Veelgestelde vragen:
1. Wat is een regressievergelijking? Antwoord: Een wiskundige representatie van de relatie tussen variabelen.
2. Hoe vind ik de beste regressievergelijking? Antwoord: Door verschillende modellen te vergelijken en de beste te selecteren op basis van statistische criteria.
3. Wat is lineaire regressie? Antwoord: Een type regressieanalyse waarbij de relatie tussen variabelen lineair is.
4. Wat is meervoudige regressie? Antwoord: Een type regressieanalyse met meerdere onafhankelijke variabelen.
5. Wat is R-kwadraat? Antwoord: Een maat voor hoe goed het model de data past.
6. Wat zijn residuals? Antwoord: Het verschil tussen de geobserveerde waarden en de voorspelde waarden.
7. Wat is overfitting? Antwoord: Wanneer het model te goed past bij de trainingsdata maar slecht presteert op nieuwe data.
8. Hoe kan ik regressieanalyse gebruiken in mijn werk? Antwoord: Om voorspellingen te maken, relaties te begrijpen en beslissingen te nemen op basis van data.
Kortom, het vinden van een regressievergelijking is een essentiële vaardigheid voor iedereen die met data werkt. Het biedt een krachtige manier om relaties tussen variabelen te analyseren, voorspellingen te doen en inzicht te krijgen in complexe fenomenen. Door de principes van regressieanalyse te begrijpen en de juiste technieken toe te passen, kunnen we waardevolle informatie halen uit data en betere beslissingen nemen. Door de continue ontwikkeling van statistische software en de toenemende beschikbaarheid van data, wordt regressieanalyse steeds toegankelijker en relevanter voor een breed scala aan toepassingen. Het beheersen van deze techniek is daarom een waardevolle investering voor iedereen die geïnteresseerd is in data-analyse en het ontrafelen van de geheimen die verborgen liggen in de data.

how to find regression equation | Kennecott Land

Linear Regression in R | Kennecott Land

How to Quickly Find Regression Equation in Excel | Kennecott Land

Excel linear regression meaning | Kennecott Land

How to Find Regression Equation in Excel | Kennecott Land

Simple linear regression equation example | Kennecott Land

Linear Equation Line Regression at Robert Sirois blog | Kennecott Land

how to find regression equation | Kennecott Land

Simple linear regression equation myomlab | Kennecott Land

Criterion Variable Definition Use and Examples | Kennecott Land

Linear equation regression calculator | Kennecott Land

Updated Learning How To Find Equation Of Regression Line E6F | Kennecott Land
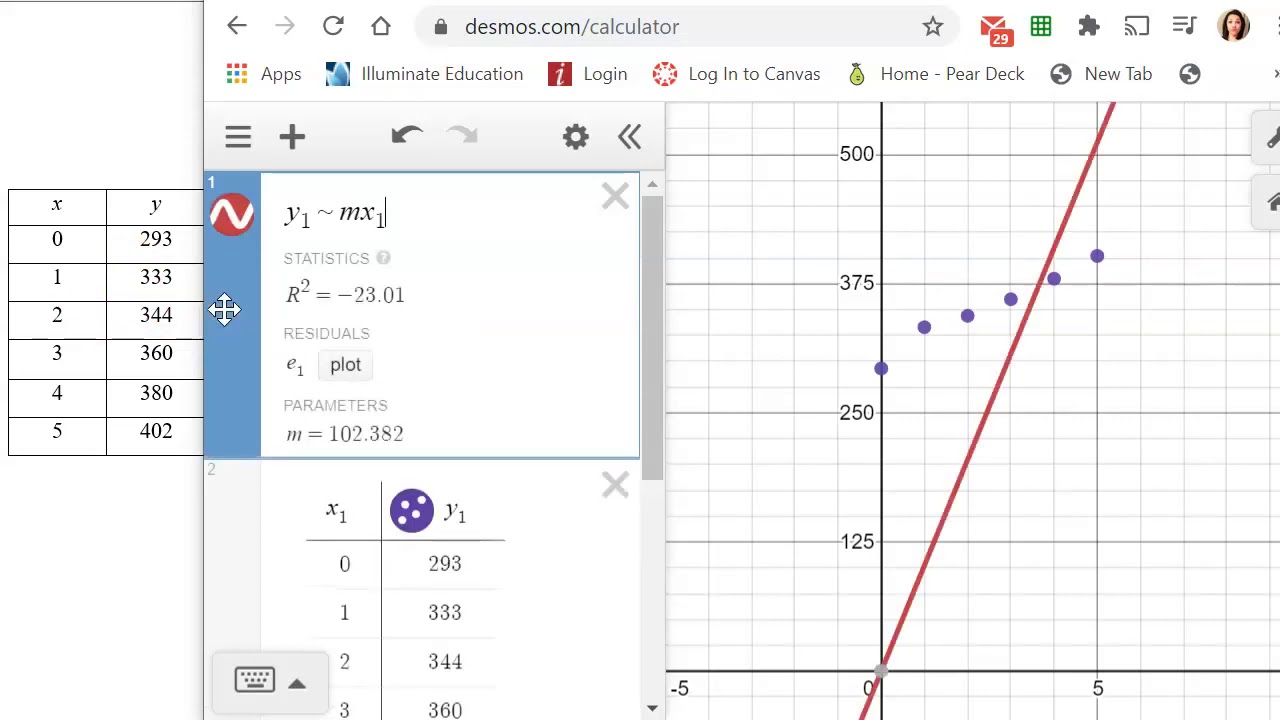
Calculate linear regression equation | Kennecott Land
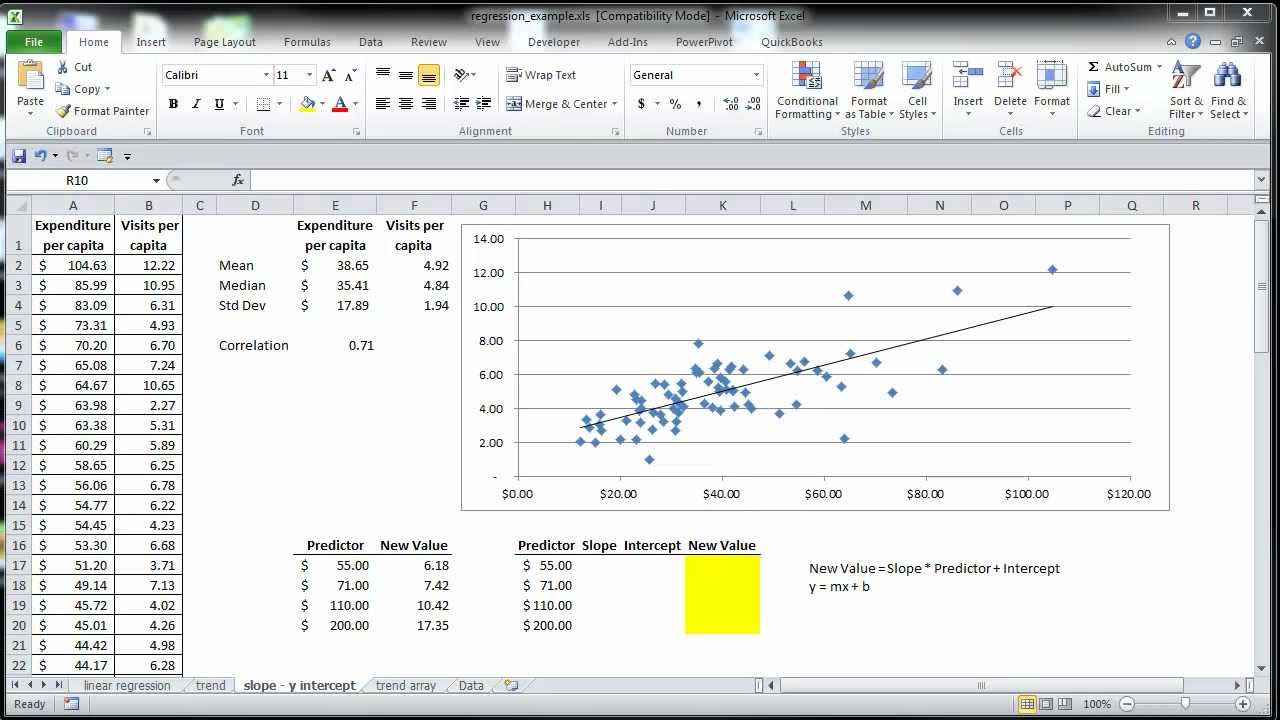
Simple linear regression excel | Kennecott Land

how to find regression equation | Kennecott Land