Trigonometrie ontrafeld: Berekening Sin Cos Tan
Stel je voor: je bent aan het wandelen en ziet een hoge boom. Je vraagt je af hoe hoog die boom eigenlijk is. Met een beetje trigonometrie en de hulp van "berechnung sin cos tan" kun je die hoogte berekenen! Deze drie trigonometrische functies - sinus, cosinus en tangens - vormen de basis voor het begrijpen van hoeken en zijden in driehoeken.
Van het meten van afstanden tot het modelleren van golven, "berechnung sin cos tan" is overal in de wetenschap en techniek te vinden. De oorsprong van deze functies gaat terug tot de oude Grieken, die ze gebruikten voor astronomie en navigatie. Vandaag de dag vormen ze de ruggengraat van vakgebieden zoals architectuur, muziek en computergraphics.
Het belang van "berechnung sin cos tan" ligt in hun vermogen om relaties tussen hoeken en zijden in rechthoekige driehoeken te beschrijven. Met behulp van deze functies kunnen we onbekende zijden of hoeken berekenen, zolang we maar voldoende informatie hebben. Dit maakt ze ongelooflijk nuttig voor het oplossen van problemen in de echte wereld.
Laten we eens kijken naar een voorbeeld. Stel je voor dat je de hoogte van een gebouw wilt bepalen. Je meet de afstand van het gebouw (de basis van de driehoek) en de hoek tussen de grond en de top van het gebouw (de hoek tegenover de onbekende zijde). Met behulp van de tangensfunctie (tan = overstaande zijde / aanliggende zijde) kun je de hoogte van het gebouw berekenen.
Naast het bepalen van afstanden, heeft "berechnung sin cos tan" tal van andere toepassingen. In de natuurkunde worden ze gebruikt om de beweging van projectielen te beschrijven, terwijl ze in de muziek helpen bij het begrijpen van geluidsgolven. In de computergraphics worden ze gebruikt om 3D-modellen te maken en te manipuleren. Kortom, de toepassingen van "berechnung sin cos tan" zijn eindeloos!
Voordelen van "Berechnung Sin Cos Tan"
Het gebruik van "berechnung sin cos tan" biedt talloze voordelen in verschillende disciplines:
- Problemen met driehoeken oplossen: Bereken onbekende zijden en hoeken in rechthoekige driehoeken.
- Modelleren van periodieke verschijnselen: Beschrijf golfachtige patronen in gebieden zoals muziek, natuurkunde en engineering.
- Navigatie en plaatsbepaling: Bereken afstanden en richtingen in de luchtvaart, scheepvaart en GPS-systemen.
Tips en Tricks voor "Berechnung Sin Cos Tan"
Om "berechnung sin cos tan" effectief te gebruiken, zijn hier een paar handige tips:
- Ken je formules: Zorg ervoor dat je de formules voor sinus, cosinus en tangens goed kent.
- Maak een schets: Teken een diagram van de driehoek om de gegeven informatie en de onbekende waarde te visualiseren.
- Gebruik een rekenmachine: Gebruik een wetenschappelijke rekenmachine om de waarden van trigonometrische functies te berekenen.
Conclusie
"Berechnung sin cos tan" speelt een cruciale rol in ons begrip van trigonometrie en zijn toepassingen in de echte wereld. Of je nu een student, wetenschapper of gewoon nieuwsgierig bent naar de wereld om je heen, het begrijpen van sinus, cosinus en tangens opent een wereld van mogelijkheden. Blijf deze functies verkennen en ontdek hun kracht bij het oplossen van problemen en het ontrafelen van de mysteries van de wereld!

berechnung sin cos tan | Kennecott Land

berechnung sin cos tan | Kennecott Land

Rechenwege Sinus, kosinus und tanens? (Schule, Mathematik) | Kennecott Land

Trigonometrie Erklärung mit Formeln und Beispielen | Kennecott Land

berechnung sin cos tan | Kennecott Land

Flächeninhalt eines Dreiecks | Kennecott Land

berechnung sin cos tan | Kennecott Land

HTWG Konstanz, Fakultät Maschinenbau, Studiengang MEP 1 Übungen | Kennecott Land
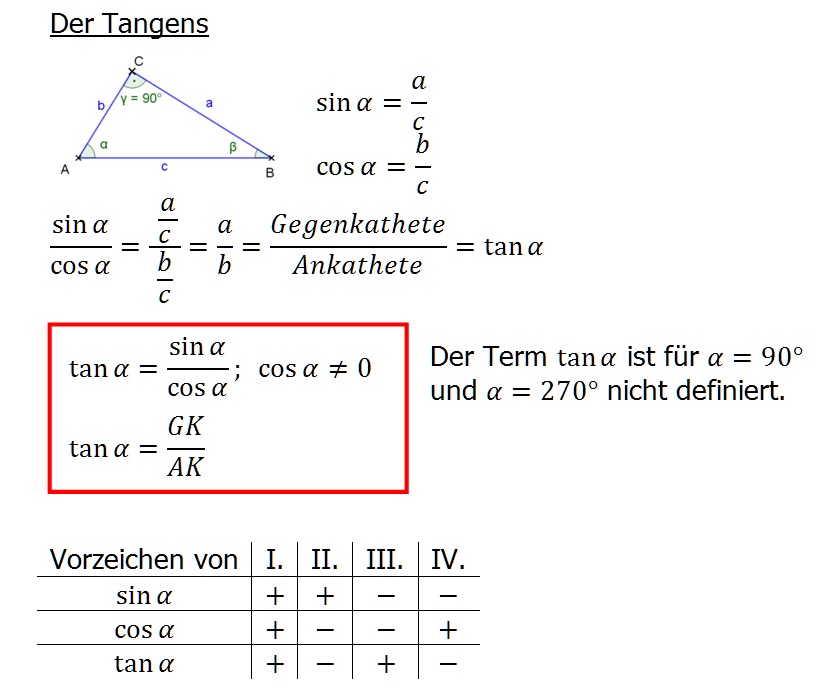
berechnung sin cos tan | Kennecott Land

berechnung sin cos tan | Kennecott Land

berechnung sin cos tan | Kennecott Land

Trigonometric table Stock Vector Images | Kennecott Land

berechnung sin cos tan | Kennecott Land

berechnung sin cos tan | Kennecott Land

berechnung sin cos tan | Kennecott Land