Phasor Transformation: Simplifying Circuit Analysis
Ever wrestled with complex sinusoidal functions in circuit analysis? There's a more elegant solution: phasor transformation. This powerful technique simplifies AC circuit calculations by replacing cumbersome sinusoidal functions with complex numbers, making analysis much more manageable. Imagine trading trigonometric identities for basic algebra – that's the magic of phasor conversion.
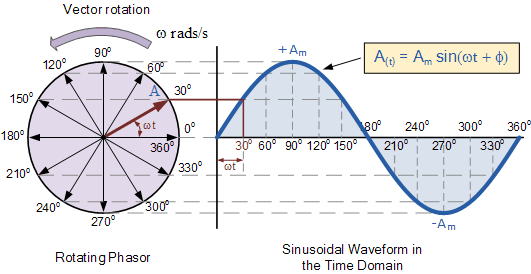
Phasor notation represents a sinusoidal function as a complex number, effectively freezing the oscillating wave at a specific point in time. This snapshot captures the magnitude and phase shift of the sinusoid, discarding the time-varying component. This simplified representation allows engineers to analyze circuits using algebraic techniques rather than complex differential equations, speeding up calculations and providing clearer insights.
The concept of phasor representation stems from Euler's formula, which establishes a relationship between complex exponentials and trigonometric functions. This mathematical link allows sinusoidal functions to be expressed in a complex exponential form, from which the phasor is readily extracted. This mathematical foundation solidifies the validity and robustness of the phasor transformation method.
Phasor transformation is a cornerstone of electrical engineering, enabling simplified analysis of AC circuits crucial for power systems, communication systems, and electronic circuit design. Without this tool, analyzing circuits with sinusoidal sources would be significantly more complex and time-consuming. Imagine designing a power grid without the efficiency of phasor calculations – it would be a herculean task.
However, using phasor transformation requires a good understanding of complex numbers and the underlying principles. Common pitfalls include errors in converting between time-domain and phasor-domain representations, particularly in handling phase shifts correctly. Moreover, remembering the frequency dependence of impedances in phasor analysis is critical for accurate results.
Representing a sinusoidal function like Acos(ωt + φ) in phasor form involves capturing its amplitude (A) and phase angle (φ) as a complex number A∠φ or A(cos φ + jsin φ). For example, 10cos(100t + 30°) becomes 10∠30° in phasor form.
Three key benefits of using a phasor conversion calculator are: 1) Speed: Quickly convert between time-domain and phasor representations, saving valuable time. 2) Accuracy: Minimize manual calculation errors, ensuring precise results. 3) Clarity: Simplify complex expressions, leading to a clearer understanding of circuit behavior.
To successfully apply phasor transformation: 1) Identify the sinusoidal function. 2) Extract its amplitude and phase angle. 3) Represent the phasor in either polar or rectangular form. 4) Perform circuit analysis using complex algebra. 5) Convert the result back to the time domain if needed. An example: analyzing an RLC circuit using impedance in phasor form yields the circuit's steady-state response much faster than using differential equations.
Advantages and Disadvantages of Phasor Conversion
| Advantages | Disadvantages |
|---|---|
| Simplified calculations | Requires understanding of complex numbers |
| Faster analysis | Potential for phase shift errors |
| Clearer insights into circuit behavior | Not applicable for non-sinusoidal waveforms |
Five best practices: 1) Consistent Units: Ensure angles are in degrees or radians. 2) Frequency Awareness: Remember that impedance is frequency-dependent. 3) Double-Check Conversions: Verify accuracy between time-domain and phasor-domain representations. 4) Visualize Phasors: Use phasor diagrams to enhance understanding. 5) Practice Regularly: Solve various examples to solidify understanding.
Frequently asked questions about phasor conversion: 1) What is a phasor? 2) Why are phasors used? 3) How do I convert to phasor form? 4) What is a phasor diagram? 5) How do I convert back to the time domain? 6) What are the limitations of phasor analysis? 7) What are some common mistakes to avoid? 8) Where can I find more resources on phasor analysis?
Tips and tricks for phasor conversion include using online phasor calculators, practicing with different types of sinusoidal functions, and visualizing phasors on a complex plane.
In conclusion, phasor transformation is a cornerstone technique in electrical engineering, enabling efficient and insightful analysis of AC circuits. Mastering this method empowers engineers to tackle complex circuit problems with relative ease, paving the way for innovation in power systems, communication networks, and electronic circuit design. While there are some challenges to overcome, such as understanding complex numbers and handling phase shifts correctly, the benefits of simplified calculations, faster analysis, and clearer circuit understanding far outweigh the learning curve. Embrace the power of phasor conversion, explore online calculators and available resources, and unlock a new level of efficiency in your circuit analysis endeavors. Don't let complex sinusoidal functions intimidate you – transform them into manageable phasors and conquer the world of AC circuits! This will streamline your workflow and give you a deeper appreciation for the elegant mathematics underlying circuit behavior.

Rectangular to Polar Form Conversion Calculator | Kennecott Land

Complex Numbers Phasors in Polar and Rectangular Form | Kennecott Land

Polar to Rectangular Form Conversion Calculator | Kennecott Land

Solved In phasor form a voltage is V310ej45 | Kennecott Land

Rectangular to Polar form Polar to Rectangular form conversion | Kennecott Land

convert to phasor form calculator | Kennecott Land

Complex Numbers Phasors in Polar and Rectangular Form | Kennecott Land

Impedance In Phasor Form | Kennecott Land
Ac Circuit Phasor Diagram Impedance | Kennecott Land

25 Polar Form and Rectangular Form Notation for Complex Numbers | Kennecott Land

SOLVED 1 Perform the following calculations and report your answer in | Kennecott Land

Rectangular to Phasor Calculator Online | Kennecott Land

Phasor Diagram 3 Phase Ac Circuit | Kennecott Land

What is Phasor and Phasor Diagram Simple Explanation | Kennecott Land

Mathematical representation of phasor in Complex form | Kennecott Land