Unlocking Quadratic Equations: Your Guide to Understanding and Solving
Remember those intriguing puzzles in school that involved an 'x' hiding behind a square? Those, my friend, were our first encounters with the fascinating world of quadratic equations. They might seem like a mathematical maze at first, but trust me, once you understand their language, they open up a whole new world of problem-solving and analytical thinking.
But what exactly are these quadratic equations, and why should we care? Imagine you're trying to figure out the perfect trajectory for a basketball shot, or perhaps you're designing a stylish archway for a building. Believe it or not, quadratic equations play a crucial role in solving these real-world scenarios. They help us model and analyze various phenomena involving parabolic curves, from the path of a projectile to the shape of a satellite dish.
Let's journey back in time for a moment. The history of quadratic equations stretches back thousands of years, with evidence of their use found in ancient Babylonian texts. These early mathematicians were fascinated by problems involving areas and sides of squares, leading them to develop ingenious methods for solving these equations. Over the centuries, mathematicians like Brahmagupta in India and al-Khwarizmi in Persia made significant contributions, refining these techniques and laying the foundation for our modern understanding.
Now, let's demystify these equations a bit. In essence, a quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually 'x') is two. Their general form is represented as ax² + bx + c = 0, where a, b, and c are constants, and 'a' cannot be zero. Each of these constants plays a role in shaping the parabolic curve representing the equation.
The beauty of quadratic equations lies in their versatility. They have applications in diverse fields like physics, engineering, computer graphics, and even finance. For instance, physicists use them to analyze motion under gravity, while engineers rely on them to design structures. In computer graphics, they help create smooth curves and realistic animations. Understanding quadratic equations empowers us to tackle real-world problems with mathematical precision.
Advantages and Disadvantages of Quadratic Equations
| Advantages | Disadvantages |
|---|---|
| Versatile applications in various fields. | Can become complex for higher-degree equations. |
| Provide accurate solutions for real-world problems. | May require advanced mathematical knowledge for complex scenarios. |
| Help develop analytical and problem-solving skills. | Sometimes, solutions may not have real-world interpretations. |
Let's wrap up our exploration with a thought-provoking question: How can we leverage the power of quadratic equations to address challenges in our own lives? From optimizing resources to designing creative solutions, the possibilities are endless. So, embrace the elegance and practicality of these mathematical wonders – you might be surprised by the insights you uncover!
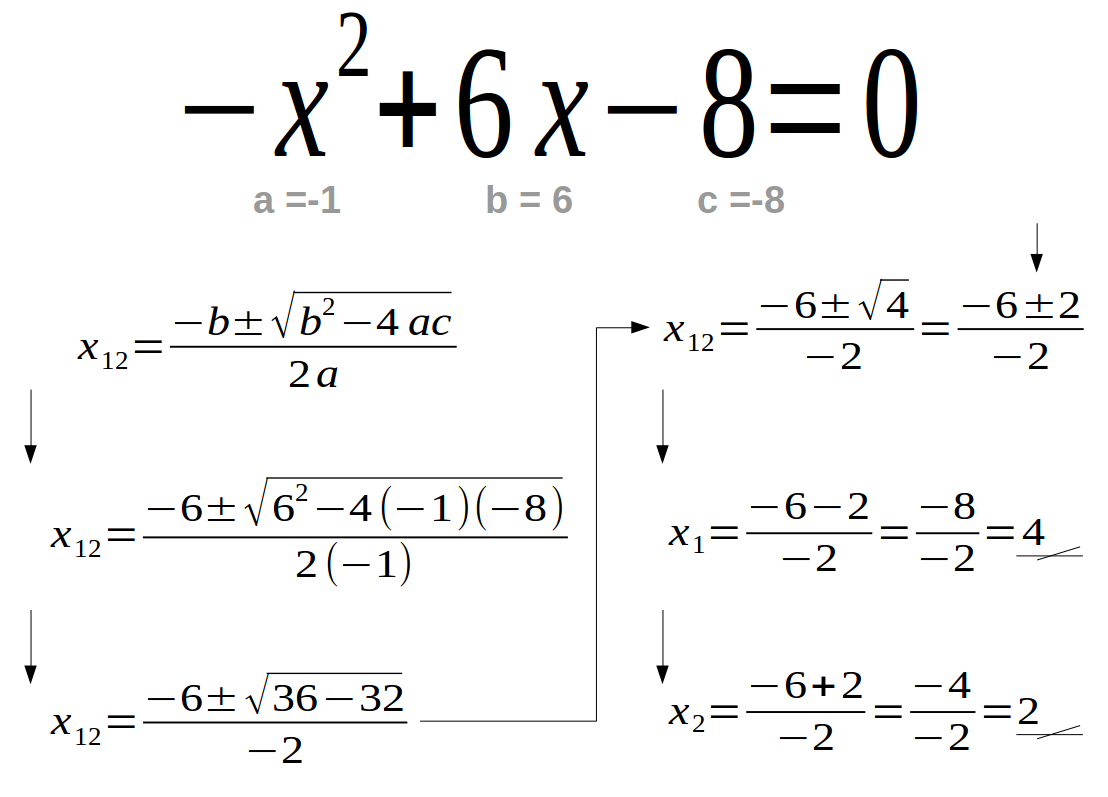
ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land
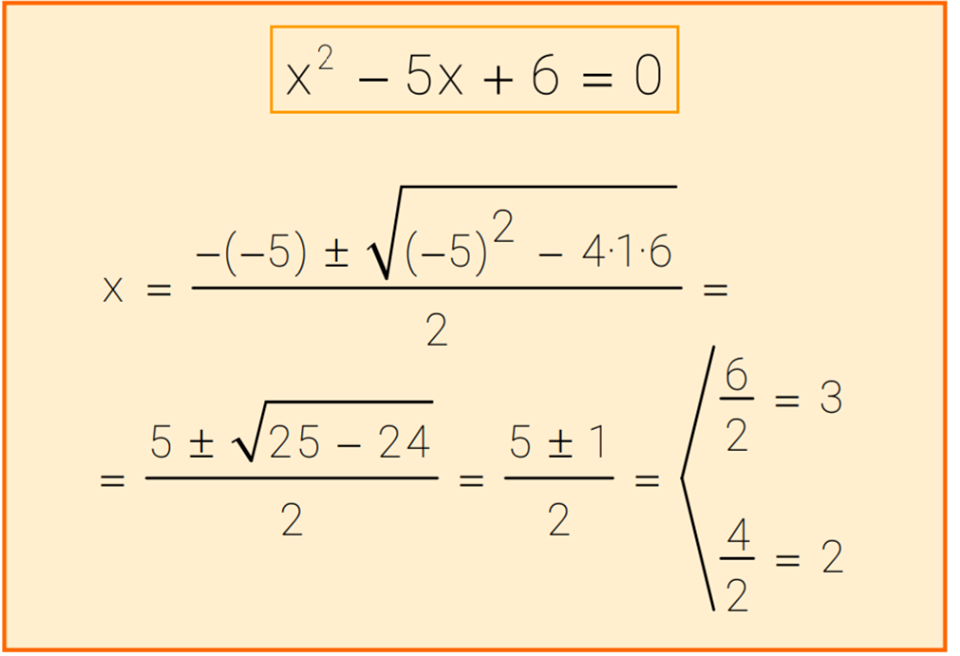
ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land

ecuaciones de 2 grado completas pdf | Kennecott Land