Unlocking the Power of Quadratic Equations: A Comprehensive Guide
Have you ever wondered how engineers calculate the perfect arc for a bridge or how economists model market trends? The answer often lies in the elegant world of quadratic equations. These mathematical expressions, with their characteristic "x squared" term, might seem intimidating at first glance. However, behind their symbolic representation lies a fascinating tool that helps us understand and solve a wide array of real-world problems.
Simply put, a quadratic equation is a polynomial equation of the second degree. This means it involves a variable raised to the power of two. The general form of a quadratic equation is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'x' is the variable we want to find. These equations have been studied for centuries, with their roots tracing back to ancient civilizations like the Babylonians and Egyptians.
The importance of quadratic equations extends far beyond the classroom. They are the backbone of numerous fields, including physics, engineering, computer graphics, and even finance. From calculating projectile motion to designing parabolic mirrors in telescopes, these equations play a crucial role in shaping our understanding of the world around us.
One of the fascinating aspects of quadratic equations is that they can have up to two distinct solutions, known as roots. These roots represent the values of 'x' for which the equation holds true. The quadratic formula, a cornerstone of algebra, provides us with a powerful tool to calculate these roots directly from the coefficients 'a', 'b', and 'c'.
Understanding quadratic equations opens up a world of possibilities. For instance, in physics, these equations are used to model the motion of objects under gravity. By plugging in the initial velocity and launch angle of a projectile, we can accurately predict its trajectory and range. Similarly, in finance, quadratic equations help analyze and predict market trends, allowing investors to make informed decisions.
Advantages and Disadvantages of Using Quadratic Equations
| Advantages | Disadvantages |
|---|---|
| Provide precise solutions for a wide range of problems | Can be complex to solve for those unfamiliar with algebraic manipulation |
| Applicable in diverse fields, demonstrating their versatility | Solutions may not always have real-world interpretations, requiring careful analysis |
| Relatively straightforward to solve using the quadratic formula or factoring methods | Limited to modeling relationships involving variables raised to the second power |
In conclusion, quadratic equations, while seemingly abstract mathematical concepts, hold immense practical value. Their ability to model and solve a diverse range of problems makes them essential tools in numerous fields, shaping our technological advancements and understanding of the world. By grasping the fundamentals of quadratic equations and their applications, we unlock a deeper appreciation for the elegance and power of mathematics in action.

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land
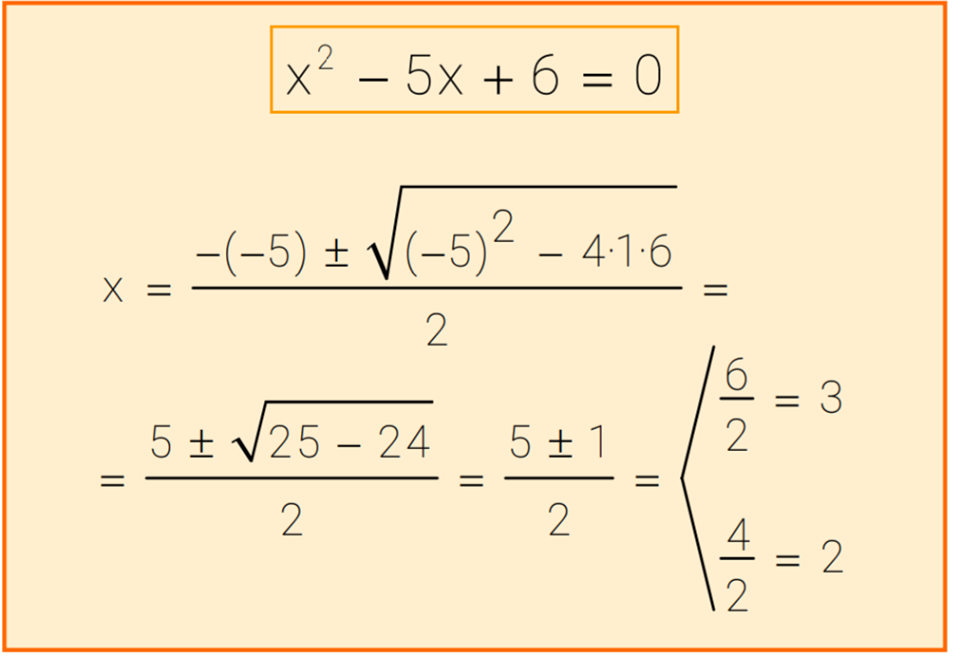
que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land

que son las ecuaciones de 2 grado | Kennecott Land